Question

【题目】在三棱柱ABC﹣A1B1C1中，侧棱BB1⊥底面A1B1C1 ， D为AC 的中点，A1B1=BB1=2，A1C1=BC1 ， ∠A1C1B=60°．
（Ⅰ）求证：AB1∥平面BDC1；
（Ⅱ）求多面体A1B1C1DBA的体积．

Answer 1

【答案】（Ⅰ）证明：连B1C交BC1于O，连接OD，在△CAB1中，O，D分别是B1C，AC的中点，∴OD∥AB1 ， 而AB1平面BDC1 ， OD平面BDC1 ， ∴AB1∥平面BDC1；
（Ⅱ）解：连接A1B，作BC的中点E，连接DE，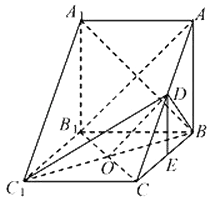

∵A1C1=BC1 ， ∠A1C1B=60°，
∴△A1C1B为等边三角形，
∵侧棱BB1⊥底面A1B1C1 ，
∴BB1⊥A1B1 ， BB1⊥B1C1 ，
∴A1C1=BC1=A1B=2 ，
∴B1C1=2，
∴A1C12=B1C12+A1B12 ，
∴∠A1B1C1=90°，∴A1B1⊥B1C1 ，
∴A1B1⊥平面B1C1CB，
∵DE∥AB∥A1B1 ，
∴DE⊥平面B1C1CB，
∴DE是三棱锥D﹣BCC1的高，
∴ = = ，
∴多面体A1B1C1DBA的体积V= ﹣ =（ ）×2﹣ = ．
【解析】（Ⅰ）证明AB1∥平面BDC1 ， 证明OD∥AB1即可；（Ⅱ）利用割补法，即可求多面体A1B1C1DBA的体积．
【考点精析】解答此题的关键在于理解直线与平面平行的判定的相关知识，掌握平面外一条直线与此平面内的一条直线平行，则该直线与此平面平行；简记为：线线平行，则线面平行．