ĖâÄŋÄÚČÝ
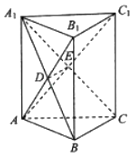
ĄūĖâÄŋĄŋÄģķŊÎïÔ°ŌŠÎŠļÕČëÔ°ĩÄÐĄķŊÎï―ĻÔėŌŧžäÁ―ÃæŋŋĮ―ĩÄČý―ĮÐÎÂķĖėŧîķŊĘŌĢŽĩØÃæÐÎŨīČįÍžËųĘūĢŽŌŅÖŠŌŅÓÐÁ―ÃæĮ―ĩÄžÐ―ĮΊ ![]() ĢĻĄÏACB=
ĢĻĄÏACB= ![]() ĢĐĢŽĮ―ABĩÄģĪķČΊ6ÃŨĢŽĢĻŌŅÓÐÁ―ÃæĮ―ĩÄŋÉĀûÓÃģĪķČŨãđŧīóĢĐĢŽžĮĄÏABC=ĶČ
ĢĐĢŽĮ―ABĩÄģĪķČΊ6ÃŨĢŽĢĻŌŅÓÐÁ―ÃæĮ―ĩÄŋÉĀûÓÃģĪķČŨãđŧīóĢĐĢŽžĮĄÏABC=ĶČ 
ĢĻ1ĢĐČôĶČ= ![]() ĢŽĮóĄũABCĩÄÖÜģĪĢĻ―áđûūŦČ·ĩ―0.01ÃŨĢĐĢŧ
ĢŽĮóĄũABCĩÄÖÜģĪĢĻ―áđûūŦČ·ĩ―0.01ÃŨĢĐĢŧ
ĢĻ2ĢĐΊÁËĘđÐĄķŊÎïÄÜ―ĄŋĩģÉģĪĢŽŌŠĮóËų―ĻĩÄČý―ĮÐÎÂķĖėŧîķŊĘŌÃæŧýĄũABCĩÄÃæŧýūĄŋÉÄÜīóĢŽÎĘĩąĶČΊšÎÖĩĘąĢŽļÃŧîķŊĘŌÃæŧýŨîīóĢŋēĒĮóģöŨîīóÃæŧýĢŪ
Ąūīð°ļĄŋ
ĢĻ1ĢĐ―âĢšÔÚĄũABCÖÐĢŽÓÉÕýÏŌķĻĀíŋÉĩÃAC= ![]() =2
=2 ![]() ĢŽBC=
ĢŽBC= ![]() =3
=3 ![]() +
+ ![]() ĢŽ
ĢŽ
ĄāĄũABCĩÄÖÜģĪΊ6+3 ![]() +3
+3 ![]() ĄÖ17.60ÃŨ
ĄÖ17.60ÃŨ
ĢĻ2ĢĐ―âĢšÔÚĄũABCÖÐĢŽÓÉÓāÏŌķĻĀíĢšc2=602=a2+b2Đ2abcos60ĄãĢŽ
Ąāa2+b2Đab=36ĢŽ
Ąā36+ab=a2+b2ĄÝ2abĢŽžīabĄÜ36ĢŽ
ĄāSĄũABC= ![]() ACBCsin
ACBCsin ![]() =
= ![]() abĄÜ9
abĄÜ9 ![]() ĢŽ
ĢŽ
īËĘąa=bĢŽĄũABCΊĩČąßČý―ĮÐÎĢŽ
ĄāĶČ=60ĄãĢŽĢĻSĄũABCĢĐmax=9 ![]()
Ąū―âÎöĄŋĢĻ1ĢĐÔÚĄũABCÖÐĢŽÓÉÕýÏŌķĻĀíŋÉĩÃACĢŽBCĢŽžīŋÉĮóĄũABCĩÄÖÜģĪĢŧĢĻ2ĢĐĀûÓÃÓāÏŌķĻĀíÁÐģöđØÏĩĘ―ĢŽ―ŦcĢŽcosCĩÄÖĩīúČëēĒĀûÓÃŧųąūēŧĩČĘ―ĮóģöabĩÄŨîīóÖĩĢŽĀûÓÃČý―ĮÐÎĩÄÃæŧýđŦĘ―ĮóģöÃæŧýĩÄŨîīóÖĩĢŽŌÔž°īËĘąĶČĩÄÖĩĢŪ

 ūŦÓĒŋÚËãŋĻÏĩÁÐīð°ļ
ūŦÓĒŋÚËãŋĻÏĩÁÐīð°ļ ÓĶÓÃĖâĩãēĶÏĩÁÐīð°ļ
ÓĶÓÃĖâĩãēĶÏĩÁÐīð°ļĄūĖâÄŋĄŋÄģÉĖģĄÎŠŌŧÖÖÔū―øÉĖÆ·―øÐКÏĀíķĻžÛĢŽ―ŦļÃÉĖÆ·°īĘÂÏČÄâķĻĩÄžÛļņ―øÐÐĘÔÏúĢŽĩÃĩ―ČįÏÂĘýūÝĢš
ĩĨÎŧ | 8 | 8.2 | 8.4 | 8.6 | 8.8 | 9 |
ÏúÁŋ | 90 | 84 | 83 | 80 | 75 | 68 |
ĢĻ1ĢĐ°īÕÕÉÏĘöĘýūÝĢŽĮóËÄđéÖąÏß·―ģĖ![]() ĢŽÆäÖÐ
ĢŽÆäÖÐ![]() ĢŽ
ĢŽ![]() Ģŧ
Ģŧ
ĢĻ2ĢĐÔĪžÆÔÚ―ņšóĩÄÏúĘÛÖÐĢŽÏúÁŋÓëĩĨÎŧČÔČŧ·þīÓĢĻĒņĢĐÖÐĩÄđØÏĩĢŽČôļÃÉĖÆ·ĩÄģÉąūĘĮÃŋžþ7.5ÔŠĢŽÎŠĘđÉĖģĄŧņĩÃŨîīóĀûČóĢŽļÃÉĖÆ·ĩÄĩĨžÛÓĶķĻΊķāÉŲÔŠĢŋĢĻĀûČó=ÏúĘÛĘÕČëĐģÉąūĢĐ
ĄūĖâÄŋĄŋÄģÉĖĩęΊÁËļüšÃĩØđæŧŪÄģÖÖÉĖÆ·―øŧõĩÄÁŋĢŽļÃÉĖĩęīÓÄģŌŧÄęĩÄÏúĘÛĘýūÝÖÐĢŽËæŧúģéČĄÁË![]() ŨéĘýūÝŨũΊŅÐūŋķÔÏóĢŽČįÏÂÍžËųĘūĢĻ
ŨéĘýūÝŨũΊŅÐūŋķÔÏóĢŽČįÏÂÍžËųĘūĢĻ![]() ĢĻķÖĢĐΊļÃÉĖÆ·―øŧõÁŋĢŽ
ĢĻķÖĢĐΊļÃÉĖÆ·―øŧõÁŋĢŽ ![]() ĢĻĖėĢĐΊÏúĘÛĖėĘýĢĐĢš
ĢĻĖėĢĐΊÏúĘÛĖėĘýĢĐĢš
| 2 | 3 | 4 | 5 | 6 | 8 | 9 | 11 |
| 1 | 2 | 3 | 3 | 4 | 5 | 6 | 8 |
ĢĻĒņĢĐļųūÝÉÏąíĘýūÝÔÚÏÂÁÐÍøļņÖÐŧæÖÆÉĒĩãÍžĢŧ
ĢĻĒōĢĐļųūÝÉÏąíĖáđĐĩÄĘýūÝĢŽĮóģö![]() đØÓÚ
đØÓÚ![]() ĩÄÏßÐÔŧØđé·―ģĖ
ĩÄÏßÐÔŧØđé·―ģĖ![]() Ģŧ
Ģŧ
ĢĻĒó)ÔÚļÃÉĖÆ·―øŧõÁŋ![]() ĢĻķÖĢĐēŧģŽđý6ĢĻķÖĢĐĩÄĮ°ĖáÏÂČÎČĄÁ―ļöÖĩĢŽĮóļÃÉĖÆ·―øŧõÁŋxĢĻķÖĢĐĮĄÓÐŌŧļöÖĩēŧģŽđý3ĢĻķÖĢĐĩÄļÅÂĘ.
ĢĻķÖĢĐēŧģŽđý6ĢĻķÖĢĐĩÄĮ°ĖáÏÂČÎČĄÁ―ļöÖĩĢŽĮóļÃÉĖÆ·―øŧõÁŋxĢĻķÖĢĐĮĄÓÐŌŧļöÖĩēŧģŽđý3ĢĻķÖĢĐĩÄļÅÂĘ.
ēÎŋžđŦĘ―šÍĘýūÝĢš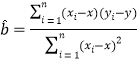 ĢŽ
ĢŽ![]() ĢŪ
ĢŪ![]()