题目内容
【题目】已知向量 
， 
，函数 
．
（1）求函数f（x）的单调递增区间；
（2）已知a，b，c分别为△ABC内角A，B，C的对边，其中A为锐角， 
，c=1，且f（A）=1，求△ABC的面积S．
【答案】
（1）解： 
= 
= 
= 
= 
=sin（2x﹣ 
），
由 
（k∈z），
函数f（x）的单调递增区间为 
（k∈z）．
（2）解： 
，
因为 
， 
，所以. 
， 
，
又a2=b2+c2﹣2bccosA，则b=2，
从而 
【解析】（1）利用向量的数量积的运算，以及两角和二倍角公式化简函数的表达式，通过正弦函数的单调增区间求解即可．（2）利用（1）的结果，推出A的大小，然后利用余弦定理求出b，利用三角形的面积公式求解即可．
【题目】在高中学习过程中，同学们经常这样说“如果物理成绩好，那么学习数学就没什么问题”某班针对“高中生物理对数学学习的影响”进行研究，得到了学生的物理成绩与数学成绩具有线性相关关系的结论，现从该班随机抽取5名学生在一次考试中的物理和数学成绩，如表：
编号 | 1 | 2 | 3 | 4 | 5 |
物理（x） | 90 | 85 | 74 | 68 | 63 |
数学（y） | 130 | 125 | 110 | 95 | 90 |
（参考公式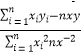：b= 
， 
= 
b 
，）参考数据：902+852+742+682+632=29394
90×130+85×125+74×110+68×95+63×90=42595．
（1）求数学y成绩关于物理成绩x的线性回归方程 
= 
x+ （b精确到0.1），若某位学生的物理成绩为80分时，预测他的物理成绩．
（2）要从抽取的这五位学生中随机选出三位参加一项知识竞赛，以X表示选中的学生的数学成绩高于100分的人数，求随机变量X的分布列及数学期望．
【题目】某商场为一种跃进商品进行合理定价，将该商品按事先拟定的价格进行试销，得到如下数据：
单位 | 8 | 8.2 | 8.4 | 8.6 | 8.8 | 9 |
销量 | 90 | 84 | 83 | 80 | 75 | 68 |
（1）按照上述数据，求四归直线方程
，其中
，
；
（2）预计在今后的销售中，销量与单位仍然服从（Ⅰ）中的关系，若该商品的成本是每件7.5元，为使商场获得最大利润，该商品的单价应定为多少元？（利润=销售收入﹣成本）
