题目内容
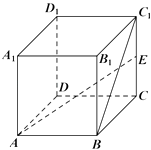
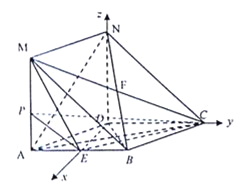
【题目】在如图所示的几何体中,四边形ABCD是菱形,ADNM是矩形,平面ADNM⊥平面ABCD,∠DAB=60°,AD=2,AM=1,E为AB的中点.
(Ⅰ)求证:AN∥平面MEC;
(Ⅱ)在线段AM上是否存在点P,使二面角P﹣EC﹣D的大小为![]() ?若存在,求出AP的长h;若不存在,请说明理由.
?若存在,求出AP的长h;若不存在,请说明理由.

【答案】(1)见解析(2)![]()
【解析】试题分析:
(1)利用题意证得AN∥EF,结合线面平行的判断定理可得AN∥平面MEC;
(2)建立空间直角坐标系可得,存在点P满足题意,其中![]() .
.
试题解析:
(I)CM与BN交于F,连接EF.
由已知可得四边形BCNM是平行四边形,所以F是BN的中点.
因为E是AB的中点,所以AN∥EF.
又EF平面MEC,AN平面MEC,所以AN∥平面MEC.
(II)由于四边形ABCD是菱形,E是AB的中点,可得DE⊥AB.
又四边形ADNM是矩形,面ADNM⊥面ABCD,
∴DN⊥面ABCD,
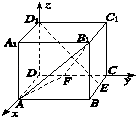
如图建立空间直角坐标系D﹣xyz,
则D(0,0,0),E(![]() ,0,0),C(0,2,0),P(
,0,0),C(0,2,0),P(![]() ,﹣1,h),
,﹣1,h),
![]() =(
=(![]() ,﹣2,0),
,﹣2,0),![]() =(0,﹣1,h),
=(0,﹣1,h),
设平面PEC的法向量为![]() =(x,y,z).
=(x,y,z).
则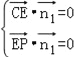 ,∴
,∴![]() ,令y=
,令y=![]() h,∴
h,∴![]() =(2h,
=(2h,![]() h,
h,![]() ),
),
又平面ADE的法向量![]() =(0,0,1),
=(0,0,1),
∴cos<![]() ,
,![]() >=
>=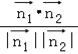 =
=![]() =
=![]() ,解得h=
,解得h=![]() ,
,
∴在线段AM上是否存在点P,当h=![]() 时使二面角P﹣EC﹣D的大小为
时使二面角P﹣EC﹣D的大小为![]() .
.

 阅读快车系列答案
阅读快车系列答案【题目】为调查高中生的数学成绩与学生自主学习时间之间的相关关系,长郡中学数学教师对新入学的45名学生进行了跟踪调查,其中每周自主做数学题的时间不少于15小时的有19人,余下的人中,在高三模拟考试中数学平均成绩不足120分的占![]() ,统计成绩后,得到如下的
,统计成绩后,得到如下的![]() 列联表:
列联表:
分数大于等于120分 | 分数不足120分 | 合计 | |
周做题时间不少于15小时 | 4 | 19 | |
周做题时间不足15小时 | |||
合计 | 45 |
(1)请完成上面的![]() 列联表,并判断能否在犯错误的概率不超过0.01的前提下认为“高中生的数学成绩与学生自主学习时间有关”;
列联表,并判断能否在犯错误的概率不超过0.01的前提下认为“高中生的数学成绩与学生自主学习时间有关”;
(2)(ⅰ)按照分层抽样的方法,在上述样本中,从分数大于等于120分和分数不足120分两组学生中抽取9名学生,设抽到的不足120分且周做题时间不足15小时的人数是![]() ,求
,求![]() 的分布列(概率用组合数算式表示);
的分布列(概率用组合数算式表示);
(ⅱ)若将频率视为概率,从全校大于等于120分的学生中随机抽取20人,求这些人中周做题时间不少于15小时的人数的期望和方差.
|
|
|
|
|
|
|
|
附: