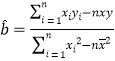题目内容
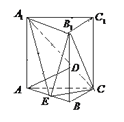
【题目】如图,正三棱柱![]() 的所有棱长均为2,
的所有棱长均为2, ![]() ,
, ![]() 分别为
分别为![]() 和
和![]() 的中点.
的中点.

(1)证明: ![]() 平面
平面![]() ;
;
(2)求点![]() 到平面
到平面![]() 的距离.
的距离.
【答案】(1)详见解析;(2) ![]() .
.
【解析】试题分析:(1)证明线面垂直,一般方法为利用线面垂直的判定定理,即从线线垂直出发给予证明,而线线垂直的寻找与论证,可从两个方面出发,一是利用面面垂直得线面垂直,再得线线垂直,二是利用平几知识,如本题中正方形有关性质,(2)求点到直线距离,一般方法为利用等体积法,即根据![]() 可得
可得![]() 分别求出两个三角形面积代入可得点
分别求出两个三角形面积代入可得点![]() 到平面
到平面![]() 的距离.
的距离.
试题解析:(I)证明:由![]() 知
知![]() ,又平面
,又平面![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() ,而
,而![]()
![]() 平面
平面 ![]() ,∴
,∴![]() ,在正方形
,在正方形![]() 中,由
中,由![]() 分别是
分别是![]() 和
和![]() 的中点知
的中点知![]() ,而
,而![]() ,∴
,∴![]() 平面
平面![]() .
.
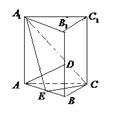
(Ⅱ)解法1: 由(I)![]() 平面
平面![]() ,过
,过![]() 点作
点作![]() , 交
, 交![]() 和
和![]() 分别于点
分别于点![]() 和
和![]() ,则
,则![]() 平面
平面![]() ,即
,即![]() 的长为
的长为![]() 到平面
到平面![]() 的距离, 在正方形
的距离, 在正方形![]() 中,易知
中,易知![]() ,
, ![]()
![]() ,即
,即![]() ,得
,得![]() ,故
,故![]() 到平面
到平面![]() 的距离为
的距离为![]() .
.
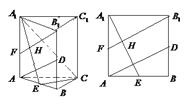
解法2:如图,连接![]() ,在三棱锥
,在三棱锥![]() 中,设
中,设![]() 到平面
到平面![]() 的距离为
的距离为![]() ,则
,则![]() ,将
,将![]() ,
, ![]() 代入得
代入得![]() ,得
,得![]() , 故
, 故![]() 到平面
到平面![]() 的距离为
的距离为![]() .
.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
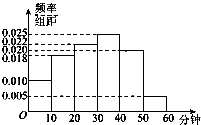
【题目】参加衡水中学数学选修课的同学,对某公司的一种产品销量与价格进行统计,得到如下数据和散点图:
定价 |
|
|
|
|
|
|
年销售 |
|
|
|
|
|
|
|
|
|
|
|
|
|
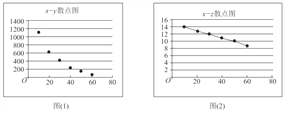
(参考数据:![]()
![]() )
)
(I)根据散点图判断,![]() 与
与![]() ,
,![]() 与
与![]() 哪一对具有较强的线性相关性(给出判断即可,不必说明理由)?
哪一对具有较强的线性相关性(给出判断即可,不必说明理由)?
(II)根据(I)的判断结果有数据,建立![]() 关于
关于![]() 的回归方程(方程中的系数均保留两位有效数字);
的回归方程(方程中的系数均保留两位有效数字);
(III)定价为多少元/![]() 时,年利润的预报值最大?
时,年利润的预报值最大?
附:对一组数据![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为:
的斜率和截距的最小二乘估计分别为: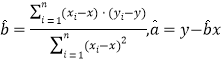 .
.