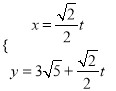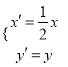题目内容
【题目】已知椭圆C: ![]() +
+ ![]() =1(a>b>0)的离心率为
=1(a>b>0)的离心率为 ![]() ,其中左焦点F(﹣2,0).
,其中左焦点F(﹣2,0).
(1)求椭圆C的方程;
(2)若直线y=x+m与椭圆C交于不同的两点A,B,且线段的中点M在圆x2+y2=1上,求m的值.
【答案】
(1)解:由题意,得 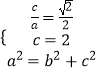
解得 ![]() ∴椭圆C的方程为
∴椭圆C的方程为 ![]() .
.
(2)解:设点A、B的坐标分别为(x1,y1),(x2,y2),线段AB的中点为M(x0,y0),
由 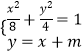 消y得,3x2+4mx+2m2﹣8=0,
消y得,3x2+4mx+2m2﹣8=0,
△=96﹣8m2>0,∴﹣2 ![]() <m<2
<m<2 ![]() .
.
∴ ![]() =﹣
=﹣ ![]() ,
,
![]() .
.
∵点M(x0,y0)在圆x2+y2=1上,∴ ![]() ,∴
,∴ ![]() .
.
【解析】(1)由题意,得 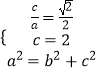 由此能够得到椭圆C的方程.(2)设点A、B的坐标分别为(x1 , y1),(x2 , y2),线段AB的中点为M(x0 , y0),由
由此能够得到椭圆C的方程.(2)设点A、B的坐标分别为(x1 , y1),(x2 , y2),线段AB的中点为M(x0 , y0),由 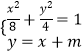 消y得,3x2+4mx+2m2﹣8=0,再由根的判断式结合题设条件能够得到m的值.
消y得,3x2+4mx+2m2﹣8=0,再由根的判断式结合题设条件能够得到m的值.

练习册系列答案
相关题目
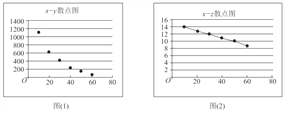
【题目】参加衡水中学数学选修课的同学,对某公司的一种产品销量与价格进行统计,得到如下数据和散点图:
定价 |
|
|
|
|
|
|
年销售 |
|
|
|
|
|
|
|
|
|
|
|
|
|
(参考数据:![]()
![]() )
)
(I)根据散点图判断,![]() 与
与![]() ,
,![]() 与
与![]() 哪一对具有较强的线性相关性(给出判断即可,不必说明理由)?
哪一对具有较强的线性相关性(给出判断即可,不必说明理由)?
(II)根据(I)的判断结果有数据,建立![]() 关于
关于![]() 的回归方程(方程中的系数均保留两位有效数字);
的回归方程(方程中的系数均保留两位有效数字);
(III)定价为多少元/![]() 时,年利润的预报值最大?
时,年利润的预报值最大?
附:对一组数据![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为:
的斜率和截距的最小二乘估计分别为: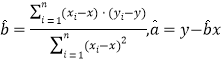 .
.