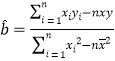题目内容
【题目】设函数f（x）=a2x+ 
（a，b，c为常数，且a＞0，c＞0）．
（1）当a=1，b=0时，求证：|f（x）|≥2c；
（2）当b=1时，如果对任意的x＞1都有f（x）＞a恒成立，求证：a+2c＞1．
【答案】
（1）解：a=1，b=0时，
f（x）=x+ 
，x＞0时，f（x）≥2 
=2c，
x＜0时，f（x）≤﹣2 
=﹣2c，
综上：|f（x）|≥2c；
（2）解：a＞0，b＞0，b=1，x＞1时，x﹣1＞0，
∴f（x）=a2x+ 
=a2（x﹣1）+ +a2
≥2ac+a2
=a（2c+a）＞a，
∴a+2c＞1．
【解析】（1）求出f（x）的表达式，根据基本不等式的性质证明即可；（2）根据基本不等式的性质证明即可．
【考点精析】解答此题的关键在于理解函数的最大(小)值与导数的相关知识，掌握求函数
在
上的最大值与最小值的步骤：（1）求函数在
内的极值；（2）将函数的各极值与端点处的函数值
，
比较，其中最大的是一个最大值，最小的是最小值．
练习册系列答案
相关题目
