题目内容
【题目】已知a≠0，集合A={x|x2﹣x﹣6＜0}，B={x|x2+2x﹣8≥0}，C={x|x2﹣4ax+3a2＜0}，且C（A∩RB）．求实数a的取值范围．
【答案】解：依题意得：A={x|﹣2＜x＜3}，B={x|x≤﹣4或x≥2}，（CRB）={x|﹣4＜x＜2}
∴A∩（CRB）=（﹣2，2）
①若a＞0，则C={x|a＜x＜3a}，
由C（A∩CRB）得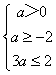 
，解得0＜a≤ 
②若a＜0，则C={x|3a＜x＜a}，
由C（A∩CRB）得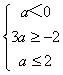 
，解得﹣ ≤a＜0
综上，实数a的取值范围为0＜a≤ 或﹣ ≤a＜0
【解析】先通过解一元二次不等式化简集合A和B，再求集合B的补集，最后求出A∩（CRB），由于一元二次方程x2﹣4ax+3a2=0的两个根是：a，3a．欲表示出集合C，须对a进行分类讨论：①若a＞0，②若a＜0，再结合C（A∩CRB），列出不等关系求得a的取值范围，最后综合得出实数a的取值范围即可．
【考点精析】本题主要考查了交、并、补集的混合运算的相关知识点，需要掌握求集合的并、交、补是集合间的基本运算，运算结果仍然还是集合，区分交集与并集的关键是“且”与“或”，在处理有关交集与并集的问题时，常常从这两个字眼出发去揭示、挖掘题设条件，结合Venn图或数轴进而用集合语言表达，增强数形结合的思想方法才能正确解答此题．
练习册系列答案
相关题目
