题目内容
【题目】若直线 l1和l2 是异面直线,l1在平面 α内,l2在平面β内,l是平面α与平面β的交线,则下列命题正确的是( )
A.l与l1 , l2都不相交
B.l与l1 , l2都相交
C.l至多与l1 , l2中的一条相交
D.l至少与l1 , l2中的一条相交
【答案】D
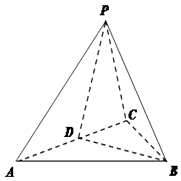
【解析】解:A.l与l1 , l2可以相交,如图:  ∴该选项错误;
∴该选项错误;
B.l可以和l1 , l2中的一个平行,如上图,∴该选项错误;
C.l可以和l1 , l2都相交,如下图: ,∴该选项错误;
,∴该选项错误;
D.“l至少与l1 , l2中的一条相交”正确,假如l和l1 , l2都不相交;
∵l和l1 , l2都共面;
∴l和l1 , l2都平行;
∴l1∥l2 , l1和l2共面,这样便不符合已知的l1和l2异面;
∴该选项正确.
故选D.
可以画出图形来说明l与l1 , l2的位置关系,从而可判断出A,B,C是错误的,而对于D,可假设不正确,这样l便和l1 , l2都不相交,这样可推出和l1 , l2异面矛盾,这样便说明D正确.

练习册系列答案
相关题目
【题目】某中学一位高三班主任对本班50名学生学习积极性和对待班级工作的态度进行调查,得到的统计数据如表所示:
积极参加班级工作 | 不积极参加班级工作 | 合计 | |
学习积极性高 | 18 | 7 | 25 |
学习积极性不高 | 6 | 19 | 25 |
合计 | 24 | 26 | 50 |
(1)如果随机调查这个班的一名学生,那么抽到不积极参加班级工作且学习积极性不高的学生的概率是多少?
(2)若不积极参加班级工作且学习积极性高的7名学生中有两名男生,现从中抽取2名学生参加某项活动,问2名学生中有1名男生的概率是多少?
(3)学生的学习积极性与对待班级工作的态度是否有关系?请说明理由.
附:

![]()