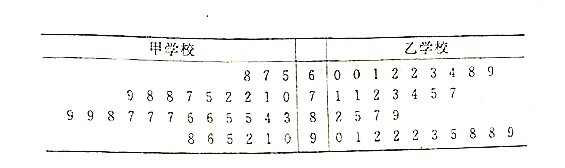
题目内容
【题目】在四棱锥P﹣ABCD中,底面ABCD是直角梯形,AD∥BC,AB⊥BC,侧面PAB⊥底面ABCD.若PA=AD=AB=kBC(0<k<1),则( ) 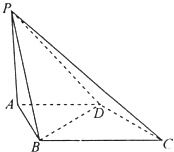
A.当k= ![]() 时,平面BPC⊥平面PCD
时,平面BPC⊥平面PCD
B.当k= ![]() 时,平面APD⊥平面PCD
时,平面APD⊥平面PCD
C.对?k∈(0,1),直线PA与底面ABCD都不垂直
D.?k∈(0,1),使直线PD与直线AC垂直.
【答案】A
【解析】解:只有A正确.下面给出证明:
延长BA,CD交于M点,连接MP,则BM=2AB,
A是BM的中点,AP= ![]() BM,
BM,
∴MP⊥PB,
又∵侧面PAB⊥底面ABCD,AB⊥BC,
∴BC⊥平面PBM,可得BC⊥MP,
故MP⊥平面PBC,
∵MP平面PCD,∴平面PBC⊥平面PCD.
可知:B,C,D都不正确.
故选:A.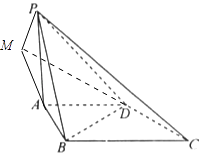
【考点精析】根据题目的已知条件,利用棱锥的结构特征的相关知识可以得到问题的答案,需要掌握侧面、对角面都是三角形;平行于底面的截面与底面相似,其相似比等于顶点到截面距离与高的比的平方.

练习册系列答案
相关题目