题目内容
【题目】在正三棱柱ABC﹣A1B1C1中,若AB1⊥BC1 , 则下列关于直线A1C和AB1 , BC1的关系的判断正确的为( )
A.A1C和AB1 , BC1都垂直
B.A1C和AB1垂直,和BC1不垂直
C.A1C和AB1 , BC1都不垂直
D.A1C和AB1不垂直,和BC1垂直
【答案】A
【解析】解:设D为BC的中点,连结AD、B1D,设E为AB的中点,连结CE、A1E, ∵△ABC是正三角形,∴AD⊥BC,
由正三棱柱的性质可知,平面ABC⊥平面BB1C1C,
又平面ABC∩平面BB1C1C=BC,∴AD⊥平面BB1C1C,
∴B1D是AB1在平面BB1C1C上的射影,
同理,A1E是A1C在平面AA1B1B上的射影,
∵AB1⊥BC1 , 由三垂线逆定理可知,B1D⊥BC1 ,
∵长方形AA1B1B≌长方形BB1C1 , ∴A1E⊥AB1 , 由三垂线定理可知,AB1⊥A1C;
取AC中点F,连结BF、C1F,
∵△ABC是等边三角形,∴BF⊥AC,∵AA1⊥平面ABC,∴BF⊥AA1 ,
∵AA1∩AC=A,∴BF⊥平面ACC1A1 , ∵A1C平面ACC1A1 , ∴BF⊥A1C,
∵长方形AA1B1B≌长方形BB1C1≌长方形AA1C1C,∴A1C⊥C1F,由三垂线定理可知,BC1⊥A1C.
∴A1C和AB1 , BC1都垂直.
故选:A.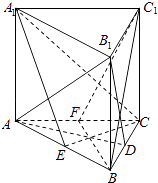
【考点精析】通过灵活运用空间中直线与平面之间的位置关系,掌握直线在平面内—有无数个公共点;直线与平面相交—有且只有一个公共点;直线在平面平行—没有公共点即可以解答此题.

练习册系列答案
相关题目