题目内容
设函数f(x)=
x3-
(2a-1)x2+[a2-a-f′(a)]x+b,(a,b∈R)
(1)求f′(a)的值;
(2)若对任意的a∈[0,1],函数f(x)在x∈[0,1]上的最小值恒大于1,求b的取值范围.
| 1 |
| 3 |
| 1 |
| 2 |
(1)求f′(a)的值;
(2)若对任意的a∈[0,1],函数f(x)在x∈[0,1]上的最小值恒大于1,求b的取值范围.
(1)∵f(X)=
x3-
(2a-1)x2+[a2-a-f(a)]x+b(a,b∈R)
∴f′(x)=x2-(2a-1)x+a2-a-f′(a),
∴f′(a)=a2-(2a-1)a+a2-a-f′(a),
∴f'(a)=0.
(2)∵f(X)=
x3-
(2a-1)x2+[a2-a-f(a)]x+b(a,b∈R)
∴f′(x)=x2-(2a-1)x+a2-a-f′(a),
∴f′(a)=a2-(2a-1)a+a2-a-f′(a),
∴f′(a)=0.
∴f′(x)=x2-(2a-1)x+(a2-a)=[x-(a-1)](x-a),
令f′(x)>0,得x<a-1,或x>a;令f′(x)<0,得a-1<x<a,
∴f(x)在(-∞,a-1]上单调递增,在[a-1,a]上单调递减,在[a,+∞)上单调递增,
∵0≤a≤1,∴f(x)在x∈[0,1]上的最小值为f(a)=
a3-
a2+b,
∴
a3-
a2+b>1在a∈[0,1]上恒成立.
即b>-
a3+
a2+1在a∈[0,1]上恒成立,
令g(x)=-
x2+
x2+1(0≤x≤1),
则g′(x)=-x2+x=-x(x-1)≥0,
∴g(x)在x∈[0,1]上单调递增,
∴1≤g(x)≤
,
∴b>
.
| 1 |
| 3 |
| 1 |
| 2 |
∴f′(x)=x2-(2a-1)x+a2-a-f′(a),
∴f′(a)=a2-(2a-1)a+a2-a-f′(a),
∴f'(a)=0.
(2)∵f(X)=
| 1 |
| 3 |
| 1 |
| 2 |
∴f′(x)=x2-(2a-1)x+a2-a-f′(a),
∴f′(a)=a2-(2a-1)a+a2-a-f′(a),
∴f′(a)=0.
∴f′(x)=x2-(2a-1)x+(a2-a)=[x-(a-1)](x-a),
令f′(x)>0,得x<a-1,或x>a;令f′(x)<0,得a-1<x<a,
∴f(x)在(-∞,a-1]上单调递增,在[a-1,a]上单调递减,在[a,+∞)上单调递增,
∵0≤a≤1,∴f(x)在x∈[0,1]上的最小值为f(a)=
| 1 |
| 3 |
| 1 |
| 2 |
∴
| 1 |
| 3 |
| 1 |
| 2 |
即b>-
| 1 |
| 3 |
| 1 |
| 2 |
令g(x)=-
| 1 |
| 3 |
| 1 |
| 2 |
则g′(x)=-x2+x=-x(x-1)≥0,
∴g(x)在x∈[0,1]上单调递增,
∴1≤g(x)≤
| 7 |
| 6 |
∴b>
| 7 |
| 6 |

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案
相关题目
 则二项式
则二项式 的常数项是 .
的常数项是 .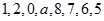 的中位数为
的中位数为 ,则直线
,则直线 与曲线
与曲线 围成图形的面积为 .
围成图形的面积为 .



 ,直线
,直线 所围图形面积S= .
所围图形面积S= .