题目内容
设函数f(x)=x3-3ax+b(a≠0).
(Ⅰ)若曲线y=f(x)在点(2,f(2))处与直线y=8相切,求a,b的值;
(Ⅱ)求函数f(x)的单调区间与极值点.
(Ⅰ)若曲线y=f(x)在点(2,f(2))处与直线y=8相切,求a,b的值;
(Ⅱ)求函数f(x)的单调区间与极值点.
(Ⅰ)f′(x)=3x2-3a,
∵曲线y=f(x)在点(2,f(2))处与直线y=8相切,
∴
⇒
⇒
(Ⅱ)∵f′(x)=3(x2-a)(a≠0),
当a<0时,f′(x)>0,函数f(x)在(-∞,+∞)上单调递增,此时函数f(x)没有极值点.
当a>0时,由f′(x)=0⇒x=±
,
当x∈(-∞,-
)时,f′(x)>0,函数f(x)单调递增,
当x∈(-
,
)时,f′(x)<0,函数f(x)单调递减,
当x∈(
,+∞)时,f′(x)>0,函数f(x)单调递增,
∴此时x=-
是f(x)的极大值点,x=
是f(x)的极小值点.
∵曲线y=f(x)在点(2,f(2))处与直线y=8相切,
∴
|
|
|
(Ⅱ)∵f′(x)=3(x2-a)(a≠0),
当a<0时,f′(x)>0,函数f(x)在(-∞,+∞)上单调递增,此时函数f(x)没有极值点.
当a>0时,由f′(x)=0⇒x=±
| a |
当x∈(-∞,-
| a |
当x∈(-
| a |
| a |
当x∈(
| a |
∴此时x=-
| a |
| a |

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目

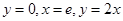 及曲线
及曲线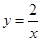 所围成的封闭的图形的面积为( )
所围成的封闭的图形的面积为( )
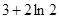


 等于( )
等于( )
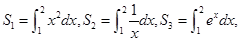 若 ,则s1,s2,s3的大小关系为( )
若 ,则s1,s2,s3的大小关系为( )