题目内容
已知函数f1(x)=
x2,f2(x)=alnx(其中a>0).
(Ⅰ)求函数f(x)=f1(x)•f2(x)的极值;
(Ⅱ)若函数g(x)=f1(x)-f2(x)+(a-1)x在区间(
,e)内有两个零点,求正实数a的取值范围;
(Ⅲ)求证:当x>0时,1nx+
-
>0.(说明:e是自然对数的底数,e=2.71828…)
| 1 |
| 2 |
(Ⅰ)求函数f(x)=f1(x)•f2(x)的极值;
(Ⅱ)若函数g(x)=f1(x)-f2(x)+(a-1)x在区间(
| 1 |
| e |
(Ⅲ)求证:当x>0时,1nx+
| 3 |
| 4x2 |
| 1 |
| ex |
解析(Ⅰ)f(x)=f1(x)•f2(x)=
x2alnx,
∴f′(x)=axlnx+
ax=
ax(2lnx+1),(x>0,a>0),
由f′(x)>0,得x>e
,由f′(x)<0,得0<x<e
.
∴函数f(x)在(0,e
)上是减函数,在(e
,+∞)上是增函数,
∴f(x)的极小值为f(e
)=-
,无极大值.
(Ⅱ)函数g(x)=
x2-alnx+(a-1)x,
则g′(x)=x-
+(a-1)=
=
,
令g′(x)=0,∵a>0,解得x=1,或x=-a(舍去),
当0<x<1时,g′(x)<0,g(x)在(0,1)上单调递减;
当x>1时,g′(x)>0,g(x)在(1,+∞)上单调递增.
函数g(x)在区间(
,e)内有两个零点,
只需
,即
,∴
,解得
<x<
,
故实数a的取值范围是(
,
).
(Ⅲ)问题等价于x2lnx>
-
,
由(I)知,f(x)=x2lnx的最小值为-
,
设h(x)=
-
,h′(x)=-
得,函数h(x)在(0,2)上增,在(2,+∞)减,
∴h(x)max=h(2)=
-
,
因-
-(
-
)=
=
>0,
∴f(x)min>h(x)max,
∴x2lnx>
-
,∴lnx-(
-
)>0,
∴lnx+
-
>0.
| 1 |
| 2 |
∴f′(x)=axlnx+
| 1 |
| 2 |
| 1 |
| 2 |
由f′(x)>0,得x>e
| 1 |
| 2 |
| 1 |
| 2 |
∴函数f(x)在(0,e
| 1 |
| 2 |
| 1 |
| 2 |
∴f(x)的极小值为f(e
| 1 |
| 2 |
| a |
| 4e |
(Ⅱ)函数g(x)=
| 1 |
| 2 |
则g′(x)=x-
| a |
| x |
| x2+(a-1)x-a |
| x |
| (x+a)(x-1) |
| x |
令g′(x)=0,∵a>0,解得x=1,或x=-a(舍去),
当0<x<1时,g′(x)<0,g(x)在(0,1)上单调递减;
当x>1时,g′(x)>0,g(x)在(1,+∞)上单调递增.
函数g(x)在区间(
| 1 |
| e |
只需
|
|
|
| 2e-1 |
| 2e2+2e |
| 1 |
| 2 |
故实数a的取值范围是(
| 2e-1 |
| 2e2+2e |
| 1 |
| 2 |
(Ⅲ)问题等价于x2lnx>
| x2 |
| ex |
| 3 |
| 4 |
由(I)知,f(x)=x2lnx的最小值为-
| 1 |
| 2e |
设h(x)=
| x2 |
| ex |
| 3 |
| 4 |
| x(x-2) |
| ex |
∴h(x)max=h(2)=
| 4 |
| e2 |
| 3 |
| 4 |
因-
| 1 |
| 2e |
| 4 |
| e2 |
| 3 |
| 4 |
| 3e2-2e-16 |
| 4e2 |
| (3e-8)(e+2) |
| 4e2 |
∴f(x)min>h(x)max,
∴x2lnx>
| x2 |
| ex |
| 3 |
| 4 |
| 1 |
| ex |
| 3 |
| 4x2 |
∴lnx+
| 3 |
| 4x2 |
| 1 |
| ex |

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
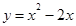 与直线
与直线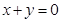 所围成的封闭图形的面积为( )
所围成的封闭图形的面积为( )



 等于( )
等于( )


