题目内容
已知函数f(x)=ax2+ln(x+1).
(1)求函数g(x)=f(x)-ax2-x的单调区间及最大值;
(2)当x∈[0,+∞)时,不等式f(x)≤x恒成立,求实数a的取值范围.
(3)求证:(1+
)(1+
)(1+
)(1+
)…(1+
)<e
参考导数公式:(ln(x+1))′=
.
(1)求函数g(x)=f(x)-ax2-x的单调区间及最大值;
(2)当x∈[0,+∞)时,不等式f(x)≤x恒成立,求实数a的取值范围.
(3)求证:(1+
| 1 |
| 22 |
| 1 |
| 3^ |
| 1 |
| 42 |
| 1 |
| 52 |
| 1 |
| n2 |
参考导数公式:(ln(x+1))′=
| 1 |
| x+1 |
(1)因为g(x)=f(x)-ax2-x=ax2+ln(x+1)-ax2-x=ln(x+1)-x(x>-1),
所以g′(x)=
-1=-
(x>-1),
当-1<x<0时,g′(x)>0,当x>0时,g′(x)<0,
故函数g(x)的单调递增区间为(-1,0),单调递减区间为(0,+∞).
g(x)max=g(0)=ln1=0.
(2)因为当x∈[0,+∞)时,不等式f(x)≤x恒成立,即ax2+ln(x+1)-x≤0恒成立,
设g(x)=ax2+ln(x+1)-x(x≥0),只需g(x)max≤0即可.
g′(x)=2ax+
-1=
,
①当a=0时,g′(x)=
,当x>0时,g′(x)<0,函数g(x)在(0,+∞)上单调递减,故g(x)≤g(0)=0成立.
②当a>0时,由g′(x)=
=0,因x∈[0,+∞),所以x=
-1,
1°若
-1<0,即a>
时,在区间(0,+∞)上,g′(x)>0,则g(x)在(0,+∞)上单调递增,
g(x)在[0,+∞)上无最大值,此时不满足条件;
2°若
-1≥0,即0<a≤
时,函数g(x)在(0,
)上单调递减,在区间(
,+∞)上单调递增,同样g(x)在[0,+∞)上无最大值,不满足条件.
③当a<0时,由g′(x)=
,∵x∈[0,+∞),∴2ax+(2a-1)<0,
∴g′(x)<0,故函数g(x)在[0,+∞)上单调递减,故g(x)≤g(0)=0成立.
综上所述,实数a的取值范围是(-∞,0].
(3)由(1)知ln(x+1)≤x,令x=
,所以ln(1+
)≤
=
<
=
-
,
所以ln(1+
)+ln(1+
)+…+ln(1+
)<(1-
)+(
-
)+…+(
-
)=1-
<1,
所以ln(1+
)(1+
)…(1+
)<1=lne,
所以(1+
)(1+
)…(1+
)<e.
所以g′(x)=
| 1 |
| x+1 |
| x |
| x+1 |
当-1<x<0时,g′(x)>0,当x>0时,g′(x)<0,
故函数g(x)的单调递增区间为(-1,0),单调递减区间为(0,+∞).
g(x)max=g(0)=ln1=0.
(2)因为当x∈[0,+∞)时,不等式f(x)≤x恒成立,即ax2+ln(x+1)-x≤0恒成立,
设g(x)=ax2+ln(x+1)-x(x≥0),只需g(x)max≤0即可.
g′(x)=2ax+
| 1 |
| x+1 |
| x[2ax+(2a-1)] |
| x+1 |
①当a=0时,g′(x)=
| -x |
| x+1 |
②当a>0时,由g′(x)=
| x[2ax+(2a-1)] |
| x+1 |
| 1 |
| 2a |
1°若
| 1 |
| 2a |
| 1 |
| 2 |
g(x)在[0,+∞)上无最大值,此时不满足条件;
2°若
| 1 |
| 2a |
| 1 |
| 2 |
| 1 |
| 2a-1 |
| 1 |
| 2a-1 |
③当a<0时,由g′(x)=
| x[2ax+(2a-1)] |
| x+1 |
∴g′(x)<0,故函数g(x)在[0,+∞)上单调递减,故g(x)≤g(0)=0成立.
综上所述,实数a的取值范围是(-∞,0].
(3)由(1)知ln(x+1)≤x,令x=
| 1 |
| n2 |
| 1 |
| n2 |
| 1 |
| n2 |
| 1 |
| n•n |
| 1 |
| (n-1)n |
| 1 |
| n-1 |
| 1 |
| n |
所以ln(1+
| 1 |
| 22 |
| 1 |
| 32 |
| 1 |
| n2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| n-1 |
| 1 |
| n |
| 1 |
| n |
所以ln(1+
| 1 |
| 22 |
| 1 |
| 32 |
| 1 |
| n2 |
所以(1+
| 1 |
| 22 |
| 1 |
| 32 |
| 1 |
| n2 |

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

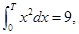 则常数T的值为 .
则常数T的值为 .