题目内容
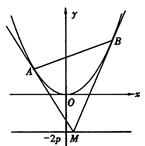
如图,设抛物线方程为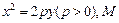 直线
直线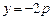 上任意一点,过M引抛物线的切线,切点分别为A,B。
上任意一点,过M引抛物线的切线,切点分别为A,B。
(1)求证:A,M,B三点的横坐标成等差数列;
(2)已知当M点的坐标为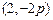 时,
时,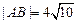 ,求此时抛物线的方程;
,求此时抛物线的方程;
(3)是否存在点M,使得点C关于直线AB的对称点D在抛物线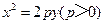 上,其中,点C满足
上,其中,点C满足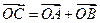 (O为坐标原点).若存在,求出所有适合题意的点M的坐标;若不存在,请说明理由.
(O为坐标原点).若存在,求出所有适合题意的点M的坐标;若不存在,请说明理由.
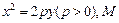 直线
直线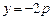 上任意一点,过M引抛物线的切线,切点分别为A,B。
上任意一点,过M引抛物线的切线,切点分别为A,B。(1)求证:A,M,B三点的横坐标成等差数列;
(2)已知当M点的坐标为
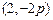 时,
时,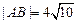 ,求此时抛物线的方程;
,求此时抛物线的方程;(3)是否存在点M,使得点C关于直线AB的对称点D在抛物线
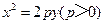 上,其中,点C满足
上,其中,点C满足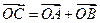 (O为坐标原点).若存在,求出所有适合题意的点M的坐标;若不存在,请说明理由.
(O为坐标原点).若存在,求出所有适合题意的点M的坐标;若不存在,请说明理由.(1)证明:由题意设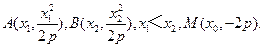
由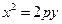 得
得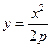 ,则
,则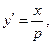
所以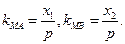
因此直线MA的方程为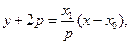 直线MB的方程为
直线MB的方程为
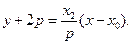
所以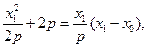 ①;
①;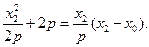 ②
②
由①-②得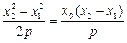 ,而
,而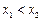 ,因此
,因此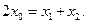
所以A、M、B三点的横坐标成等差数列.
(2)解:由(1)知,当x0=2时,
将其代入①、②并整理得: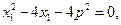
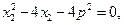
所以 x1、x2是方程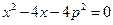 的两根,
的两根,
因此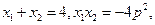 又
又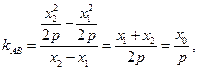 所以
所以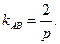
由弦长公式得: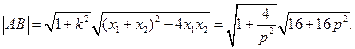
又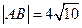 ,所以p=1或p=2,
,所以p=1或p=2,
因此所求抛物线方程为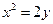 或
或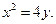
(3)解:设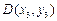 ,由题意得
,由题意得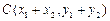
则CD的中点坐标为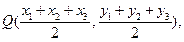
设直线AB的方程为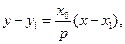
由点Q在直线AB上,并注意到点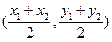 也在直线AB上,
也在直线AB上,
代入得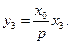
若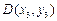 在抛物线上,则
在抛物线上,则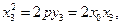
因此 x3=0或x3=2x0.即D(0,0)或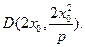
(1)当x0=0时,则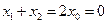 ,此时,点M
,此时,点M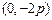 适合题意.
适合题意.
(2)当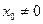 ,对于D(0,0),此时
,对于D(0,0),此时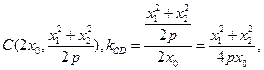
又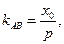 AB⊥CD,所以
AB⊥CD,所以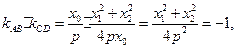
即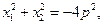 矛盾.
矛盾.
对于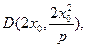 因为
因为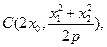 此时直线CD平行于y轴,又
此时直线CD平行于y轴,又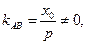
所以直线AB与直线CD不垂直,与题设矛盾,
所以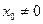 时,不存在符合题意的M点.
时,不存在符合题意的M点.
综上所述,仅存在一点M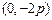 适合题意.
适合题意.
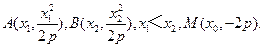

由
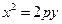 得
得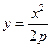 ,则
,则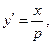
所以
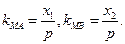
因此直线MA的方程为
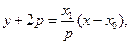 直线MB的方程为
直线MB的方程为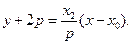
所以
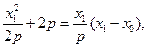 ①;
①;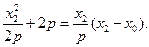 ②
②由①-②得
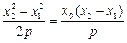 ,而
,而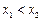 ,因此
,因此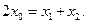
所以A、M、B三点的横坐标成等差数列.
(2)解:由(1)知,当x0=2时,
将其代入①、②并整理得:
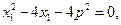
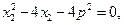
所以 x1、x2是方程
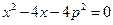 的两根,
的两根,因此
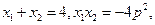 又
又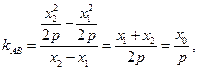 所以
所以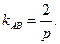
由弦长公式得:
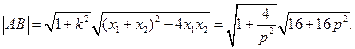
又
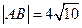 ,所以p=1或p=2,
,所以p=1或p=2,因此所求抛物线方程为
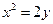 或
或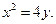
(3)解:设
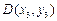 ,由题意得
,由题意得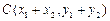
则CD的中点坐标为
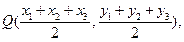
设直线AB的方程为
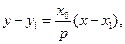
由点Q在直线AB上,并注意到点
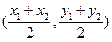 也在直线AB上,
也在直线AB上,代入得
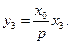
若
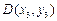 在抛物线上,则
在抛物线上,则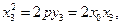
因此 x3=0或x3=2x0.即D(0,0)或
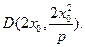
(1)当x0=0时,则
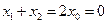 ,此时,点M
,此时,点M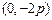 适合题意.
适合题意.(2)当
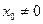 ,对于D(0,0),此时
,对于D(0,0),此时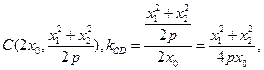
又
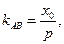 AB⊥CD,所以
AB⊥CD,所以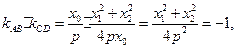
即
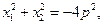 矛盾.
矛盾.对于
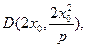 因为
因为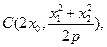 此时直线CD平行于y轴,又
此时直线CD平行于y轴,又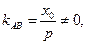
所以直线AB与直线CD不垂直,与题设矛盾,
所以
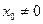 时,不存在符合题意的M点.
时,不存在符合题意的M点.综上所述,仅存在一点M
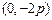 适合题意.
适合题意.略

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
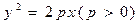 的对称轴上一点
的对称轴上一点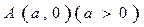 的直线与抛物线相交于M、N两点,自M、N向直线
的直线与抛物线相交于M、N两点,自M、N向直线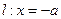 作垂线,垂足分别为
作垂线,垂足分别为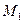 、
、 。
。 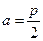 时,求证:
时,求证: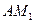 ⊥
⊥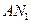 ;
;
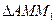 、
、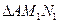 、
、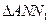 的面积分别为
的面积分别为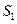 、
、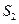 、
、 ,是否存在
,是否存在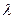 ,使得对任意的
,使得对任意的 ,都有
,都有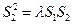 成立。若存在,求
成立。若存在,求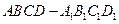 是棱长为
是棱长为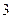 的正方体,点
的正方体,点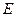 在
在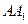 上,点
上,点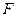 在
在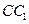 上,且
上,且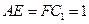 .
.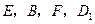 四点共面;(4分)
四点共面;(4分)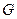 在
在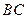 上,
上,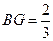 ,点
,点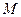 在
在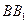 上,
上,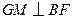 ,垂足为
,垂足为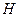 ,求证:
,求证: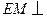 平面
平面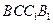 ;(4分)
;(4分)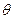 表示截面
表示截面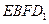 和侧面
和侧面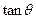 .(4分
.(4分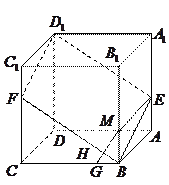
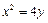 上一点
上一点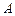 的纵坐标为4,则点
的纵坐标为4,则点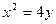 的焦点为F,
的焦点为F,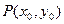 为抛物线上的任一点(其中
为抛物线上的任一点(其中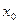 ≠0),[
≠0),[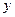 轴于Q点.
轴于Q点.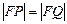 ;
;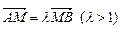 ,求
,求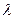 的值.
的值.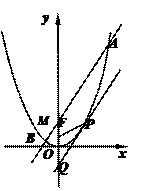
 ,直线
,直线 :
: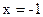 ,
, 为平面上的动点,过点
为平面上的动点,过点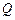 ,且
,且 .(1)求动点
.(1)求动点 轨迹
轨迹 的方程;
的方程; ,试推断:动直线DE是否过定点?证明你的结论。
,试推断:动直线DE是否过定点?证明你的结论。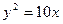 的焦点到准线的距离是( )
的焦点到准线的距离是( )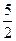 B
B 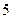 C
C 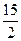
 D
D 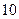
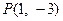 的抛物线的标准方程是
的抛物线的标准方程是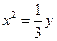 或
或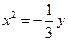
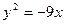 或
或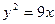
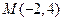 和抛物线
和抛物线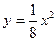 的焦点F,在抛物线上求一点P使|PM|+|PF|的值最小,则
的焦点F,在抛物线上求一点P使|PM|+|PF|的值最小,则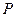 点的坐标是
点的坐标是 。
。