题目内容
1. 如图,ABCD是正方形,O是正方形的中心,PO⊥底面ABCD,E是PC的中点.
如图,ABCD是正方形,O是正方形的中心,PO⊥底面ABCD,E是PC的中点.求证:(1)PA∥平面BDE
(2)若四棱锥P-ABCD的所有棱长都等于a,求BE与平面ABCD所成角的正弦值.
分析 (1)连接OE,证明OE∥PA,即可证明PA∥平面BDE
(2)若四棱锥P-ABCD的所有棱长都等于a,取OC的中点F,连接EF,∠EBF是BE与平面ABCD所成的角,根据三角形的边角关系即可求BE与平面ABCD所成角的正弦值.
解答 证明:(1)连接OE,∵E是PC的中点.O是AC的中点.
∴OE∥PA,
∵OE?平面BDE
PA?平面BDE,
∴PA∥平面BDE.
(2)若四棱锥P-ABCD的所有棱长都等于a,
∴各侧面都是边长为a的等腰三角形,
∵PO⊥底面ABCD,
∴平面PAC⊥底面ABCD,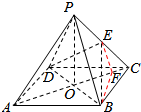
取OC的中点F,连接EF,
则EF∥PO,
且EF⊥底面ABCD,
则BF是BE在平面ABCD上的射影,
则∠EBF是BE与平面ABCD所成的角,
∵OC=OB=$\frac{\sqrt{2}a}{2}$,
∴PO=$\sqrt{P{B}^{2}-O{B}^{2}}$=$\sqrt{{a}^{2}-(\frac{\sqrt{2}a}{2})^{2}}$=$\frac{\sqrt{2}a}{2}$,
则EF=$\frac{1}{2}OP=\frac{\sqrt{2}a}{4}$,BE=$\frac{\sqrt{3}a}{2}$
则sin∠EBF=$\frac{EF}{BE}$=$\frac{\frac{\sqrt{2}a}{4}}{\frac{\sqrt{3}a}{2}}=\frac{\sqrt{6}}{6}$.
点评 本题主要考查直线和平面平行的判定,以及直线和平面所成角的求解,利用相应的判定定理和定义是解决本题的关键.

练习册系列答案
相关题目
12.已知α,β是平面,a,b是直线,则下列命题中不正确的是( )
| A. | 若a∥b,a⊥α,则b⊥α | B. | 若a∥α,α∩β=b,则a∥b | ||
| C. | 若a⊥α,a⊥β,则α∥β | D. | 若a⊥α,a?β,则α⊥β |
6.某校本学期迎来了某师范大学数学系甲、乙、丙、丁共4名实习教师,若将这4名实习教师分配到高一年级编号为1,2,3,4的4个班级实习,每班安排1名实习教师,且甲教师要安排在1班或2班,则不同的分配方案有( )
| A. | 6种 | B. | 9种 | C. | 12种 | D. | 24种 |
11.变量x,y满足$\left\{\begin{array}{l}{x-y+2≥0}\\{x+y≥0}\\{x≤0}\end{array}\right.$,目标函数z=2x+y,则z的最小值是( )
| A. | -$\frac{1}{2}$ | B. | 0 | C. | 1 | D. | -1 |