题目内容
11．变量x，y满足$\left\{\begin{array}{l}{x-y+2≥0}\\{x+y≥0}\\{x≤0}\end{array}\right.$，目标函数z=2x+y，则z的最小值是（ ）| A． | -$\frac{1}{2}$ | B． | 0 | C． | 1 | D． | -1 |
分析 先画出满足条件的平面区域，将z=2x+y变形为：y=-2x+z，平移直线得直线过A点时，z取得最小值，求出即可．
解答 解：画出满足条件的平面区域，如图示：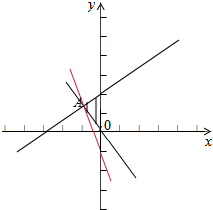
，
由z=2x+y得：y=-2x+z，
平移直线y=-2x+z，显然直线过A点时，z最小，
由$\left\{\begin{array}{l}{x-y+2=0}\\{x+y=0}\end{array}\right.$，解得：A（-1，1），
∴z最小值=-1，
故选：D．
点评 本题考查了简单的线性规划问题，考查数形结合思想，是一道基础题．
练习册系列答案
阅读快车系列答案
相关题目
如图，ABCD是正方形，O是正方形的中心，PO⊥底面ABCD，E是PC的中点．
已知[x]表示不大于x的最大整数，如[5，3]=5，[-1]=-1，执行如图的程序框图，则输出的i的值为6．
如图，矩形ABCD的两条对角线相交于点M（3，5），AB边所在直线的方程为x-3y+8=0，点N（0，6）在AD边所在直线上．
16．不等式x2＜x+6的解集为（ ）
| A． | {x|x＜-2或x＞3} | B． | {x|x＜-2} | C． | {x|-2＜x＜3} | D． | {x|x＞3} |