题目内容
11.已知数列{an}的前n项和为Sn,且满足Sn=$\frac{n+3}{2}$-an(n∈N+).(Ⅰ)计算a1,a2,a3,a4;
(Ⅱ)猜想数列{an}的通项公式an,并用数学归纳法加以证明.
分析 (Ⅰ)利用Sn=3-$\frac{n+3}{n+1}$an(n∈N*).代入计算,可得结论;
(Ⅱ)猜想an=$\frac{n+1}{{2}^{n}}$,(n∈N*).然后利用归纳法进行证明,检验n=1时等式成立,假设n=k时命题成立,证明当n=k+1时命题也成立.
解答 解:(Ⅰ) a1=1,a2=$\frac{3}{4}$,a3=$\frac{5}{8}$,a4=$\frac{9}{16}$
(Ⅱ) 由此猜想an=$\frac{{2}^{n-1}+1}{{2}^{n}}$.
证明:①当n=1时,a1=1,结论成立.
②假设n=k(k≥2且k∈N*)时,结论成立,即ak=$\frac{{2}^{k-1}+1}{{2}^{k}}$,
那么n=k+1时,ak+1=sk+1-sk=$\frac{(k+1)+3}{2}$-ak+1-$\frac{k+3}{2}$+ak=$\frac{1}{2}$+ak-ak+1,
所以ak+1=$\frac{\frac{1}{2}+\frac{{2}^{k-1}+1}{{2}^{k}}}{2}$=$\frac{{2}^{k-1}+{2}^{k-1}+1}{2•{2}^{k}}$=$\frac{{2}^{k}+1}{{2}^{k+1}}$,
这表明n=k+1时,结论成立,
由①②知an=$\frac{{2}^{n-1}+1}{{2}^{n}}$(n∈N+)成立.
点评 此题主要考查归纳法的证明,归纳法一般三个步骤:(1)验证n=1成立;(2)假设n=k成立;(3)利用已知条件证明n=k+1也成立,从而求证,这是数列的通项一种常用求解的方法

练习册系列答案
相关题目
6.有甲、乙、丙、丁四位同学参加比赛,其中只有一位获奖.关于获奖,四人如此说:甲说“是乙或丙获奖”,乙说“甲、丙都未获奖”,丙说“我获奖了”,丁说“是乙获奖”.但这四个人只有两人说得正确,请分析获奖同学是( )
| A. | 甲 | B. | 乙 | C. | 丙 | D. | 丁 |
3.如图是“推理与证明”的知识结构图,如果要加入“归纳”,则应该放在( )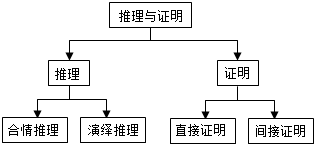

| A. | “合情推理”的下位 | B. | “演绎推理”的下位 | ||
| C. | “直接证明”的下位 | D. | “间接证明”的下位 |
20.从甲地去乙地有3班火车,从乙地去丙地有2班轮船,甲到丙地再无其他路可走,则从甲地去丙地可选择的旅行方式有( )
| A. | 5种 | B. | 6种 | C. | 7种 | D. | 8种 |
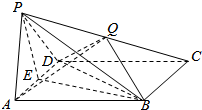 如图,四棱锥P-ABCD中,底面ABCD是菱形,PA=PD,∠BAD=60°,E是AD的中点,点Q在侧棱PC上.
如图,四棱锥P-ABCD中,底面ABCD是菱形,PA=PD,∠BAD=60°,E是AD的中点,点Q在侧棱PC上.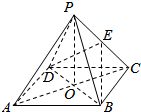 如图,ABCD是正方形,O是正方形的中心,PO⊥底面ABCD,E是PC的中点.
如图,ABCD是正方形,O是正方形的中心,PO⊥底面ABCD,E是PC的中点.