题目内容
10.已知角α是钝角,且sinα=$\frac{3}{5}$.求cosα、tanα和cos2α+sin(π+α)的值.分析 由α为钝角,根据sinα的值求出cosα的值,进而求出tanα的值,原式利用诱导公式及二倍角的余弦函数公式化简,将各自的值代入计算即可求出值.
解答 解:∵α为钝角,sinα=$\frac{3}{5}$,
∴cosα=-$\sqrt{1-si{n}^{2}α}$=-$\frac{4}{5}$,tanα=$\frac{sinα}{cosα}$=-$\frac{3}{4}$,
则原式=1-2sin2α-sinα=-$\frac{8}{25}$.
点评 此题考查了同角三角函数基本关系的运用,以及二倍角的余弦函数公式,熟练掌握运算法则是解本题的关键.

练习册系列答案
 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案
相关题目
20.从甲地去乙地有3班火车,从乙地去丙地有2班轮船,甲到丙地再无其他路可走,则从甲地去丙地可选择的旅行方式有( )
| A. | 5种 | B. | 6种 | C. | 7种 | D. | 8种 |
18.已知函数f(x)=-$\sqrt{3}$sin2x+sinxcosx.
(1)求f($\frac{π}{6}$)的值;
(2)求函数f(x)的最小正周期及最大值.
(3)求函数f(x)的单调递增区间.
(1)求f($\frac{π}{6}$)的值;
(2)求函数f(x)的最小正周期及最大值.
(3)求函数f(x)的单调递增区间.
15.二进制数1011(2)化为十进制数的结果为( )
| A. | 11 | B. | 9 | C. | 19 | D. | 13 |
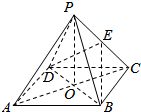 如图,ABCD是正方形,O是正方形的中心,PO⊥底面ABCD,E是PC的中点.
如图,ABCD是正方形,O是正方形的中心,PO⊥底面ABCD,E是PC的中点.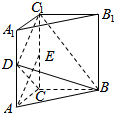 如图,三棱柱ABC-A1B1C1中,侧棱垂直于底面,∠ACB=90°,AC=$\frac{1}{2}$AA1,D、E分别是棱AA1、CC1的中点.
如图,三棱柱ABC-A1B1C1中,侧棱垂直于底面,∠ACB=90°,AC=$\frac{1}{2}$AA1,D、E分别是棱AA1、CC1的中点.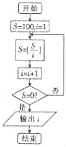 已知[x]表示不大于x的最大整数,如[5,3]=5,[-1]=-1,执行如图的程序框图,则输出的i的值为6.
已知[x]表示不大于x的最大整数,如[5,3]=5,[-1]=-1,执行如图的程序框图,则输出的i的值为6.