题目内容
13.(x-1)3+(x-1)4的展开式中含x2项的系数等于3.分析 由条件利用二项式展开式的通项公式,求得开式中含x2项的系数.
解答 解:(x-1)3+(x-1)4 的展开式中含x2项的系数等于 ${C}_{3}^{1}$•(-1)+${C}_{4}^{2}$=-3+6=3,
故答案为:3.
点评 本题主要考查二项式定理的应用,二项式展开式的通项公式,属于基础题.

练习册系列答案
相关题目
3.如图是“推理与证明”的知识结构图,如果要加入“归纳”,则应该放在( )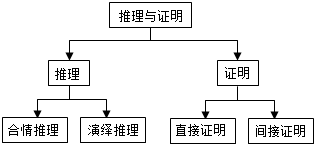

| A. | “合情推理”的下位 | B. | “演绎推理”的下位 | ||
| C. | “直接证明”的下位 | D. | “间接证明”的下位 |
4.设△ABC的角A,B,C所对的边分别是a,b,c,若$2acosB=c,sinAsinB={\frac{1}{2}}$,则△ABC为( )
| A. | 等边三角形 | B. | 等腰直角三角形 | ||
| C. | 锐角非等边三角形 | D. | 钝角三角形 |
8.二项式($\frac{1}{\sqrt{x}}$-$\frac{x}{2}$)9展开式中的常数项为( )
| A. | -$\frac{21}{2}$ | B. | $\frac{21}{2}$ | C. | 14 | D. | -14 |
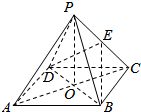 如图,ABCD是正方形,O是正方形的中心,PO⊥底面ABCD,E是PC的中点.
如图,ABCD是正方形,O是正方形的中心,PO⊥底面ABCD,E是PC的中点.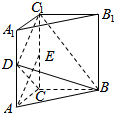 如图,三棱柱ABC-A1B1C1中,侧棱垂直于底面,∠ACB=90°,AC=$\frac{1}{2}$AA1,D、E分别是棱AA1、CC1的中点.
如图,三棱柱ABC-A1B1C1中,侧棱垂直于底面,∠ACB=90°,AC=$\frac{1}{2}$AA1,D、E分别是棱AA1、CC1的中点.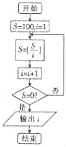 已知[x]表示不大于x的最大整数,如[5,3]=5,[-1]=-1,执行如图的程序框图,则输出的i的值为6.
已知[x]表示不大于x的最大整数,如[5,3]=5,[-1]=-1,执行如图的程序框图,则输出的i的值为6.