题目内容
【题目】设函数f（x）= 
（1）令N（x）=（1+x）2﹣1+ln（1+x），判断并证明N（x）在（﹣1，+∞）上的单调性，并求N（0）；
（2）求f（x）在定义域上的最小值；
（3）是否存在实数m，n满足0≤m＜n，使得f（x）在区间[m，n]上的值域也为[m，n]？ （参考公式：[ln（1+x）′]= 
）
【答案】
（1）解：当x＞﹣1时，N′（x）=2x+2+ 
＞0
所以，N（x）在（﹣1，+∞）上是单调递增，N（0）=0
（2）解：f（x）的定义域是（﹣1，+∞）
当﹣1＜x＜0时，N（x）＜0，所以，f′（x）＜0，
当x＞0时，N（x）＞0，所以，f′（x）＞0，
所以，在（﹣1，0）上f（x）单调递减，在（0，+∞）上，f（x）单调递增，
所以，fmin=f（0）=0
（3）解：由（2）知f（x）在[0，+∞）上是单调递增函数，
若存在m，n满足条件，则必有f（m）=m，f（n）=n，
也即方程f（x）=x在[0，+∞）上有两个不等的实根m，n，
但方程f（x）=x，即 
=0只有一个实根x=0，
所以，不存在满足条件的实数m，n
【解析】（1）先对函数求导，由导函数在x＞﹣1时的符号判断函数的单调性，代入求N（0）的值，（2）直接求定义域，利用f（x）单调性求解函数f（x）的最小值、值域，（3）假设存在符合条件的m，n则有 
，推导可判断m，n是否存在．
【考点精析】解答此题的关键在于理解利用导数研究函数的单调性的相关知识，掌握一般的,函数的单调性与其导数的正负有如下关系： 在某个区间
内，(1)如果
，那么函数
在这个区间单调递增；(2)如果
，那么函数
在这个区间单调递减，以及对函数的最大(小)值与导数的理解，了解求函数在
上的最大值与最小值的步骤：（1）求函数在内的极值；（2）将函数的各极值与端点处的函数值
，
比较，其中最大的是一个最大值，最小的是最小值．
阅读快车系列答案
【题目】我校高二年级共2000名学生，其中男生1200人.为调查学生们的手机使用情况，采用分层抽样的方法，随机抽取100位学生每周平均使用手机上网时间的样本数据（单位：小时）.根据这100个数据，得到学生每周平均使用手机上网时间的频率分布直方图（如图所示），其中样本数据分组区间分别为
.
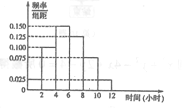
（1）应收集男生、女生样本数据各多少人？
（2）估计我校高二年级学生每周平均使用手机上网时间超过4小时的概率.
（3）将平均每周使用手机上网时间在
内定义为“长时间使用手机”，在
内定义为“短时间使用手机”.在样本数据中，有25名学生不近视.请完成下列2×2列联表，并判断是否有99.5%的把握认为“学生每周使用手机上网时间与近视程度有关”.
近视 | 不近视 | 合计 | |
长时间使用手机上网 | |||
短时间使用手机上网 | 15 | ||
合计 | 25 |
附：
| 0.100 | 0.050 | 0.010 | 0.005 |
| 2.706 | 6.635 | 7.879 |
