Question

【题目】如图，己知△BCD中，∠BCD=90°，BC=CD=1，AB⊥平面BCD，∠ADB=60°，E、F分别是AC、AD上的动点，且 =λ（0＜λ＜1）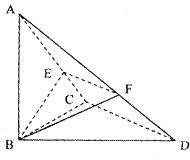
（1）求证：不论λ为何值，总有EF⊥平面ABC：
（2）若λ= ，求三棱锥A﹣BEF的体积．

Answer 1

【答案】
（1）证明：因为AB⊥平面BCD，所以AB⊥CD，

又在△BCD中，∠BCD=90°，所以，BC⊥CD，又AB∩BC=B，

所以，CD⊥平面ABC，

又在△ACD，E、F分别是AC、AD上的动点，且 =λ（0＜λ＜1）

所以，不论λ为何值，总有EF⊥平面ABC

（2）解：在△BCD中，∠BCD=90°，BC=CD=1，所以，BD= ，

又AB⊥平面BCD，所以，AB⊥BC，AB⊥BD，

又在Rt△ABC中，∠ADB=60°∴AB=BDtan60°=

由（1）知EF⊥平面ABE，∴V三棱锥A﹣BEF=V三棱锥F﹣ABE

=

所以，三棱锥A﹣BCD的体积是：

【解析】（1）要证不论λ为何值，总有EF⊥平面ABC，只需证CD⊥平面ABC，在△BCD中，根据∠BCD=90°得证．（2）根据V三棱锥A﹣BEF=V三棱锥F﹣ABE ， 得出体积即可．
【考点精析】根据题目的已知条件，利用直线与平面垂直的判定的相关知识可以得到问题的答案，需要掌握一条直线与一个平面内的两条相交直线都垂直，则该直线与此平面垂直；注意点：a)定理中的“两条相交直线”这一条件不可忽视；b)定理体现了“直线与平面垂直”与“直线与直线垂直”互相转化的数学思想．