题目内容
【题目】已知函数f(x)=ax+ ![]() ,其中函数f(x)的图象在点(1,f(1))处的切线方程为y=x﹣1.
,其中函数f(x)的图象在点(1,f(1))处的切线方程为y=x﹣1.
(1)若a= ![]() ,求函数f(x)的解析式;
,求函数f(x)的解析式;
(2)若f(x)≥g(x)在[1,+∞)上恒成立,求实数a的取值范围;
(3)证明:1+ ![]() .
.
【答案】
(1)解:f(x)的导数为f′(x)=a﹣ ![]() ,
,
则有 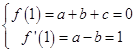 ,解得
,解得 ![]() ,
,
由a= ![]() ,得b=﹣
,得b=﹣ ![]() ,c=0,
,c=0,
故f(x)= ![]() x﹣
x﹣ ![]() ;
;
(2)解:由(1)知f(x)=ax+ ![]() +1﹣2a,
+1﹣2a,
令φ(x)=f(x)﹣g(x)=ax+ ![]() +1﹣2a﹣lnx,x∈[1,+∞),
+1﹣2a﹣lnx,x∈[1,+∞),
则φ(1)=0,φ′(x)=a﹣ ![]() ﹣
﹣ ![]() =
= 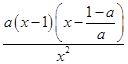 ,
,
( i)当0<a< ![]() 时,
时, ![]() >1.
>1.
若1<x< ![]() ,则φ′(x)<0,φ(x)是减函数,
,则φ′(x)<0,φ(x)是减函数,
所以φ(x)<φ(1)=0,即f(x)<g(x).
故f(x)≥g(x)在[1,+∞)上不恒成立.
(ii)当a≥ ![]() 时,
时, ![]() ≤1.
≤1.
若x>1,则φ'(x)>0,φ(x)是增函数,
所以φ(x)>φ(1)=0,即f(x)>g(x),
故当x≥1时,f(x)≥g(x).
综上所述,所求a的取值范围为[ ![]() ,+∞).
,+∞).
(3)证明:由(2)知当a≥ ![]() 时,有f(x)≥g(x)(x≥1).
时,有f(x)≥g(x)(x≥1).
令a= ![]() ,有f(x)=
,有f(x)= ![]() (x﹣
(x﹣ ![]() )≥lnx
)≥lnx
且当x>1时, ![]() (x﹣
(x﹣ ![]() )>lnx.
)>lnx.
令x= ![]() ,有ln
,有ln ![]() <
< ![]() (
( ![]() ﹣
﹣ ![]() )=
)= ![]() [(1+
[(1+ ![]() )﹣(1﹣
)﹣(1﹣ ![]() )]
)]
∴ln(k+1)﹣lnk< ![]() (
( ![]() +
+ ![]() ),k=1,2,3,…,n,
),k=1,2,3,…,n,
将上述n个不等式依次相加,得ln(n+1)< ![]() +(
+( ![]() +
+ ![]() +…+
+…+ ![]() )+
)+ ![]() ,
,
整理得1+ ![]() +
+ ![]() +…+
+…+ ![]() >ln(n+1)+
>ln(n+1)+ ![]() .
.
【解析】(1)通过函数的导数,利用导数值就是切线的斜率,切点在切线上,求出b,c,从而求出函数的解析式即可;(2)利用f(x)≥lnx,构造g(x)=f(x)﹣lnx,问题转化为g(x)=f(x)﹣lnx≥0在[1,+∞)上恒成立,利用导数求出函数在[1,+∞)上的最小值大于0,求a的取值范围;(3)由(1)可知a≥ ![]() 时,f(x)≥lnx在[1,+∞)上恒成立,则当a=
时,f(x)≥lnx在[1,+∞)上恒成立,则当a= ![]() 时,
时, ![]() (x﹣
(x﹣ ![]() )≥lnx在[1,+∞)上恒成立,对不等式的左侧每一项裂项,然后求和,即可推出要证结论.
)≥lnx在[1,+∞)上恒成立,对不等式的左侧每一项裂项,然后求和,即可推出要证结论.
【考点精析】本题主要考查了利用导数研究函数的单调性和函数的最大(小)值与导数的相关知识点,需要掌握一般的,函数的单调性与其导数的正负有如下关系: 在某个区间![]() 内,(1)如果
内,(1)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递增;(2)如果
在这个区间单调递增;(2)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递减;求函数
在这个区间单调递减;求函数![]() 在
在![]() 上的最大值与最小值的步骤:(1)求函数
上的最大值与最小值的步骤:(1)求函数![]() 在
在![]() 内的极值;(2)将函数
内的极值;(2)将函数![]() 的各极值与端点处的函数值
的各极值与端点处的函数值![]() ,
,![]() 比较,其中最大的是一个最大值,最小的是最小值才能正确解答此题.
比较,其中最大的是一个最大值,最小的是最小值才能正确解答此题.

【题目】某火锅店为了解气温对营业额的影响,随机记录了该店1月份中5天的日营业额y(单位:千元)与该地当日最低气温x(单位:℃)的数据,如表:
x | 2 | 8 | 9 | 11 | 5 |
y | 12 | 8 | 8 | 7 | 10 |
(1)求y关于x的回归方程 ![]() ;
;
(2)判定y与x之间是正相关还是负相关;若该地1月份某天的最低气温为6℃,用所求回归方程预测该店当日的营业额. (附:回归方程 ![]() 中,
中, ![]() =
= 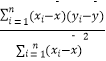 =
= 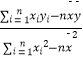 ,
, ![]() =
= ![]() ﹣
﹣ ![]() .)
.)