题目内容
【题目】在平面直角坐标系![]() 中,已知圆
中,已知圆![]() 经过
经过![]() ,
, ![]() 两点,且圆心在直线
两点,且圆心在直线![]() 上.
上.
(1)求圆![]() 的标准方程;
的标准方程;
(2)过圆![]() 内一点
内一点![]() 作两条相互垂直的弦
作两条相互垂直的弦![]() ,当
,当![]() 时,求四边形
时,求四边形![]() 的面积.
的面积.
(3)设直线![]() 与圆
与圆![]() 相交于
相交于![]() 两点,
两点, ![]() ,且
,且![]() 的面积为
的面积为![]() ,求直线
,求直线![]() 的方程.
的方程.
【答案】(1)![]() ;(2)9;(3)
;(2)9;(3)![]() 或
或![]() .
.
【解析】试题分析:(1)由圆的方程可采用待定系数法或利用圆的性质:弦的垂直平分线过圆心等来求解;(2)将四边形面积用弦长表示,利用直线与圆相交时弦长一半,圆的半径,圆心到直线的距离构成的直角三角形求解;(3)设出直线方程![]() ,将弦长和面积用
,将弦长和面积用![]() 表示,解方程可得到直线
表示,解方程可得到直线![]() 的方程
的方程
试题解析:(1)因为![]() ,
, ![]() ,所以
,所以![]() ,AB的中点为
,AB的中点为![]() ,
,
故线段AB的垂直平分线的方程为![]() ,即
,即![]() ,
,
由![]() ,解得圆心坐标为
,解得圆心坐标为![]() .
.
所以半径r满足![]() .
.
故圆![]() 的标准方程为
的标准方程为![]() .
.
(2)∵![]() ∴
∴![]() 到直线
到直线![]() 的距离相等,设为
的距离相等,设为![]()
则![]()
∴![]()
∴四边形![]() 的面积
的面积![]()
(3)设坐标原点![]() 到直线
到直线![]() 的距离为
的距离为![]() ,因为
,因为![]() .
.
①当直线![]() 与x轴垂直时,由坐标原点
与x轴垂直时,由坐标原点![]() 到直线
到直线![]() 的距离为
的距离为![]() 知,直线
知,直线![]() 的方程为
的方程为![]()
或![]() ,经验证,此时
,经验证,此时![]() ,不适合题意;
,不适合题意;
②当直线![]() 与x轴不垂直时,设直线
与x轴不垂直时,设直线![]() 的方程为
的方程为![]() ,
,
由坐标原点到直线![]() 的距离为
的距离为![]() ,得
,得![]() (*),
(*),
又圆心到直线![]() 的距离为
的距离为![]() ,所以
,所以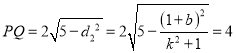 ,
,
即![]() (**),
(**),
由(*),(**)解得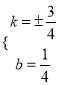 .
.
综上所述,直线![]() 的方程为
的方程为![]() 或
或![]() .
.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目