题目内容
7．已知扇形圆心角的弧度数为2，半径为3cm，则扇形的面积为（ ）| A． | 3cm2 | B． | 6cm2 | C． | 9cm2 | D． | 18cm2 |
分析 先计算扇形的弧长，再利用扇形的面积公式可求扇形的面积．
解答 解：根据扇形的弧长公式可得l=αr=6，
根据扇形的面积公式可得S=$\frac{1}{2}$lr=$\frac{1}{2}$×3×6=9．
故选：C．
点评 本题考查扇形的弧长与面积公式，正确运用公式是解题的关键．
练习册系列答案
相关题目
1．某商区停车场临时停车按时段收费，收费标准为：每辆汽车一次停车不超过1小时收费6元，超过1小时的部分每小时收费8元（不足1小时的部分按1小时计算）．现有甲、乙二人在该商区临时停车，两人停车都不超过4小时．
（Ⅰ）设甲停车付费a元．依据题意，填写下表：
（Ⅱ）若每人停车的时长在每个时段的可能性相同，求甲、乙二人停车付费之和为36元的概率；
（Ⅲ）若甲停车1小时以上且不超过2小时的概率为$\frac{1}{3}$，停车付费多于14元的概率为$\frac{5}{12}$，求甲停车付费恰为6元的概率．
（Ⅰ）设甲停车付费a元．依据题意，填写下表：
| 甲停车时长 （小时） | （0，1] | （1，2] | （2，3] | （3，4] |
| 甲停车费a （元） |
（Ⅲ）若甲停车1小时以上且不超过2小时的概率为$\frac{1}{3}$，停车付费多于14元的概率为$\frac{5}{12}$，求甲停车付费恰为6元的概率．
18．已知函数f（x）=-x2+ax-b，若a，b都是从区间[0，3]任取的一个数，则f（1）＞0成立的概率是（ ）
| A． | $\frac{2}{9}$ | B． | $\frac{4}{9}$ | C． | $\frac{5}{9}$ | D． | $\frac{8}{9}$ |
15．函数y=sin（x-$\frac{π}{4}$）cos（x-$\frac{π}{4}$）是（ ）
| A． | 最小正周期为π的奇函数 | B． | 最小正周期为π的偶函数 | ||
| C． | 最小正周期为$\frac{π}{2}$的奇函数 | D． | 最小正周期为$\frac{π}{2}$的偶函数 |
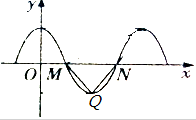函数f（x）=Acosωx（A＞0，ω＞0）部分图象如图所示，其中M，N（12，0），Q分别是函数图象在y轴右侧第一，二个零点，第一个最低点，且△MQN是等边三角形．求函数f（x）的解析式．