题目内容
2.用数学归纳法证明:求1-3+5-7+…+(-1)n-1(2n-1)=(-1)n+1n(n∈N*.分析 利用数学归纳法即可证明,注意由n=k时,正确推导n=k+1时的结论.
解答 解:(1)当n=1时,左=1,右=1,左=右,等式成立.
(2)假设n=k时,等式成立,即1-3+5-7+…+(-1)k-1(2k-1)=(-1)k+1k(k∈N*).
则当n=k+1时,1-3+5-7+…+(-1)k-1(2k-1)+(-1)k(2k+1)=(-1)k+1k+(-1)k(2k+1)=(-1)k(2k+1-k)=(-1)k+2(k+1).
∴当n=k+1时,等式成立.
根据(1)(2)说明等式1-3+5-7+…+(-1)n-1(2n-1)=(-1)n+1n(n∈N*)成立.
点评 本题考查了数学归纳法证明等式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
7.已知扇形圆心角的弧度数为2,半径为3cm,则扇形的面积为( )
| A. | 3cm2 | B. | 6cm2 | C. | 9cm2 | D. | 18cm2 |
11.由直线y=x-4,曲线y=$\sqrt{2x}$以及y=0所围成的图形的面积为( )
| A. | $\frac{40}{3}$ | B. | $\frac{34}{3}$ | C. | $\frac{64}{3}$ | D. | 16 |
12.函数y=log2x+logx(2x)的值域为( )
| A. | (-∞,-1] | B. | [3,+∞) | C. | [1,3] | D. | (-∞,-1]∪[3,+∞) |

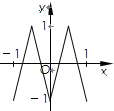
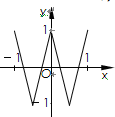
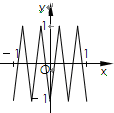
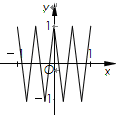
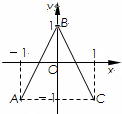 如图,函数y=f(x)的图象为折线ABC,设g(x)=f[f(x)],则函数y=g(x)的图象为( )
如图,函数y=f(x)的图象为折线ABC,设g(x)=f[f(x)],则函数y=g(x)的图象为( )