题目内容
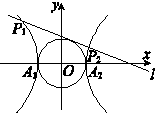
如图,已知双曲线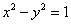 的左、右顶点分别为A1、A2,动直线l:y=kx+m与圆
的左、右顶点分别为A1、A2,动直线l:y=kx+m与圆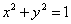 相切,且与双曲线左、右两支的交点分别为
相切,且与双曲线左、右两支的交点分别为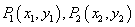 .
.
(1)求k的取值范围,并求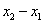 的最小值;
的最小值;
(2)记直线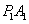 的斜率为
的斜率为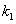 ,直线
,直线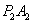 的斜率为
的斜率为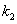 ,那么
,那么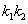 是定值吗?证明你的结论.
是定值吗?证明你的结论.
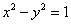 的左、右顶点分别为A1、A2,动直线l:y=kx+m与圆
的左、右顶点分别为A1、A2,动直线l:y=kx+m与圆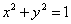 相切,且与双曲线左、右两支的交点分别为
相切,且与双曲线左、右两支的交点分别为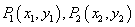 .
.
(1)求k的取值范围,并求
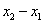 的最小值;
的最小值;(2)记直线
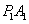 的斜率为
的斜率为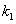 ,直线
,直线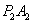 的斜率为
的斜率为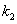 ,那么
,那么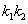 是定值吗?证明你的结论.
是定值吗?证明你的结论.(1) (-1,1) ;2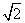 .
.
(2) 定值-(3+2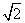 )
)
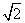 .
.(2) 定值-(3+2
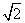 )
)(1)∵l与圆相切,∴1=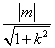
∴m2=1+k2,①
由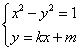 得
得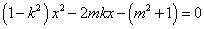 ,
,
∴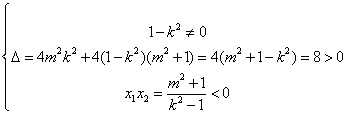
∴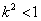 ,∴
,∴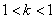 ,故k的取值范围为(-1,1).
,故k的取值范围为(-1,1).
由于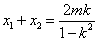 ,
,
∴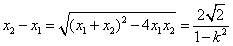 ,
,
∵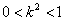 ∴当
∴当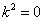 时,
时,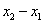 取最小值为2
取最小值为2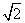 .
.
(2)由已知可得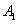 ,
,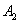 的坐标分别为(-1,0),(1,0),
的坐标分别为(-1,0),(1,0),
∴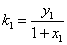 ,
,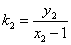 ,
,
∴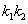 =
=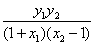 =
=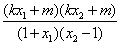
=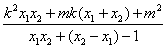
=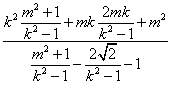
=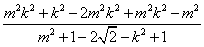 =
=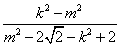 ,
,
由①,得 ,
,
∴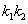 =
=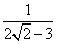 =-(3+2
=-(3+2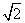 )为定值.
)为定值.
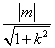
∴m2=1+k2,①
由
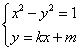 得
得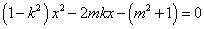 ,
,∴
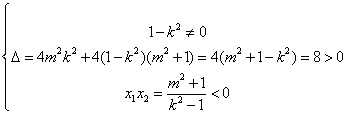
∴
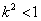 ,∴
,∴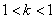 ,故k的取值范围为(-1,1).
,故k的取值范围为(-1,1).由于
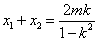 ,
,∴
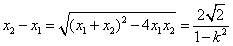 ,
,∵
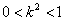 ∴当
∴当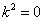 时,
时,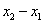 取最小值为2
取最小值为2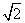 .
.(2)由已知可得
 ,
, 的坐标分别为(-1,0),(1,0),
的坐标分别为(-1,0),(1,0),∴
 ,
,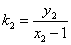 ,
,∴
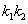 =
=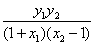 =
=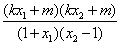
=
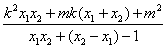
=
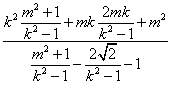
=
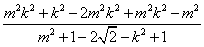 =
=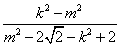 ,
,由①,得
 ,
,∴
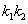 =
=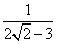 =-(3+2
=-(3+2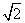 )为定值.
)为定值.
练习册系列答案
相关题目
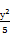 -
-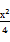 =1的一个焦点重合,则该抛物线的标准方程可能是( )
=1的一个焦点重合,则该抛物线的标准方程可能是( ) :
:
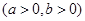 的焦距为
的焦距为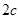 ,焦点到双曲线
,焦点到双曲线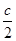 ,则双曲线
,则双曲线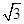

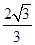
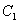 :
: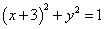 和圆
和圆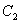 :
: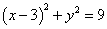 ,动圆M同时与圆
,动圆M同时与圆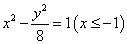
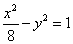
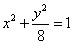
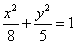
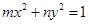 的一个焦点与抛物线
的一个焦点与抛物线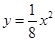 的焦点相同,离心率为2,则此双曲线的方程为
的焦点相同,离心率为2,则此双曲线的方程为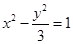
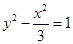
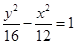
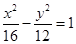
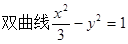 的右焦点到直线
的右焦点到直线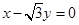 的距离是( )
的距离是( )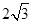
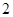
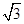
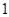
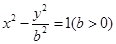 的一条渐近线的方程为
的一条渐近线的方程为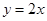 ,则
,则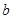 =_____ __.
=_____ __.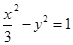 的右准线方程为 ;
的右准线方程为 ;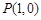 到双曲线
到双曲线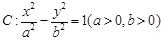 的一条渐近线的距离为
的一条渐近线的距离为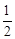 ,则双曲线
,则双曲线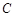 的离心率为 .
的离心率为 .