题目内容
在长方体ABCD—A1B1C1D1中,AB=4,BC=3,CC1=2,如图:
(1)求证:平面A1BC1∥平面ACD1;
(2)求(1)中两个平行平面间的距离;
(3)求点B1到平面A1BC1的距离.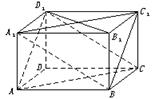
(1)求证:平面A1BC1∥平面ACD1;
(2)求(1)中两个平行平面间的距离;
(3)求点B1到平面A1BC1的距离.

(1)同解析 (2) 两平行平面间的距离为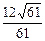 . (3) B1到平面A1BC1的距离等于
. (3) B1到平面A1BC1的距离等于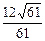 .
.
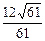 . (3) B1到平面A1BC1的距离等于
. (3) B1到平面A1BC1的距离等于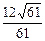 .
..(1)证明:由于BC1∥AD1,则BC1∥平面ACD1
同理,A1B∥平面ACD1,则平面A1BC1∥平面ACD1
(2)解:设两平行平面A1BC1与ACD1间的距离为d,则d等于D1到平面A1BC1的距离.易求A1C1=5,A1B=2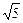 ,BC1=
,BC1=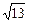 ,则cosA1BC1=
,则cosA1BC1=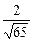 ,则sinA1BC1=
,则sinA1BC1=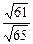 ,则S
,则S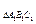 =
=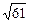 ,由于
,由于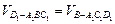 ,则
,则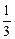 S
S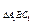 ·d=
·d=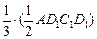 ·BB1,代入求得d=
·BB1,代入求得d=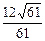 ,即两平行平面间的距离为
,即两平行平面间的距离为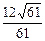 .
.
(3)解:由于线段B1D1被平面A1BC1所平分,则B1、D1到平面A1BC1的距离相等,则由(2)知点B1到平面A1BC1的距离等于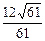 .
.
同理,A1B∥平面ACD1,则平面A1BC1∥平面ACD1
(2)解:设两平行平面A1BC1与ACD1间的距离为d,则d等于D1到平面A1BC1的距离.易求A1C1=5,A1B=2
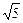 ,BC1=
,BC1=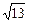 ,则cosA1BC1=
,则cosA1BC1=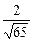 ,则sinA1BC1=
,则sinA1BC1=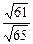 ,则S
,则S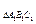 =
=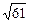 ,由于
,由于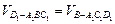 ,则
,则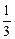 S
S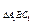 ·d=
·d=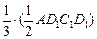 ·BB1,代入求得d=
·BB1,代入求得d=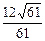 ,即两平行平面间的距离为
,即两平行平面间的距离为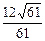 .
.(3)解:由于线段B1D1被平面A1BC1所平分,则B1、D1到平面A1BC1的距离相等,则由(2)知点B1到平面A1BC1的距离等于
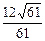 .
.
练习册系列答案
 寒假学与练系列答案
寒假学与练系列答案
相关题目
 中,E为棱CC
中,E为棱CC 上的动点,
上的动点, ⊥
⊥ ;
;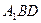 ⊥
⊥ ;
;
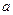 的正方体
的正方体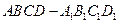 中,
中,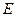 ,
,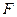 ,
,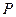 ,
,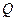 分别是
分别是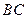 ,
,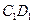 ,
,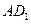 ,
,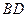 的中点.
的中点.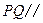 平面
平面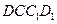 .
.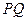 的长.
的长.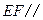 平面
平面 .
.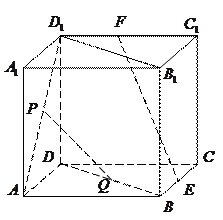
 是一个长方体,
是一个长方体, 是一个四棱锥.
是一个四棱锥. ,
,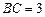 ,点
,点 且
且 .
.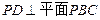 ;
; ,当
,当 为何值时,
为何值时, .
.
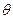 ,求sin
,求sin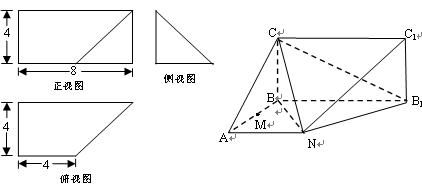
 BE;
BE;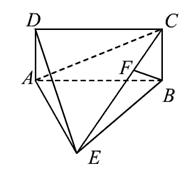
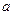 ,
,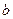 为不共面直线,
为不共面直线,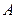 ,
,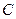 两点在
两点在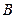 ,
,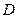 两点在
两点在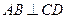 ,
,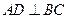 ,如图所示.求证:直线
,如图所示.求证:直线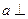 直线
直线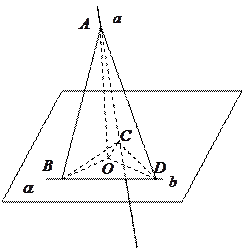
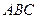
 是( )
是( )