题目内容
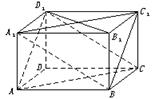
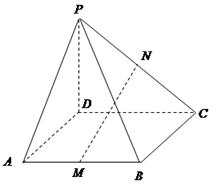
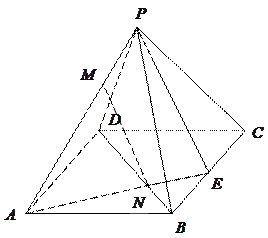
如图,在组合体中, 是一个长方体,
是一个长方体, 是一个四棱锥.
是一个四棱锥. ,
,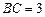 ,点
,点 且
且 .
.
(Ⅰ)证明: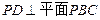 ;
;
(Ⅱ)若 ,当
,当 为何值时,
为何值时, .
.
 是一个长方体,
是一个长方体, 是一个四棱锥.
是一个四棱锥. ,
,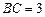 ,点
,点 且
且 .
.(Ⅰ)证明:
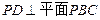 ;
;(Ⅱ)若
 ,当
,当 为何值时,
为何值时, .
.
(1)由线面垂直的判定定理,可得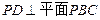
(2)当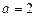 时,
时, .
.
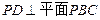
(2)当
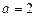 时,
时, .
. (Ⅰ)证明:因为 ,
,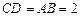 ,
,
所以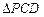 为等腰直角三角形,所以
为等腰直角三角形,所以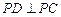 .
.
因为 是一个长方体,所以
是一个长方体,所以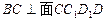 ,而
,而 ,所以
,所以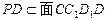 ,所以
,所以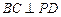 .
.
因为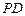 垂直于平面
垂直于平面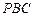 内的两条相交直线
内的两条相交直线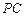 和
和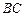 ,
,
由线面垂直的判定定理,可得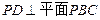
(Ⅱ)解:当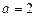 时,
时, .
.
当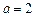 时,四边形
时,四边形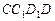 是一个正方形,所以
是一个正方形,所以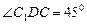 ,而
,而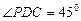 ,
,
所以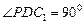 ,所以
,所以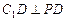 .
.
而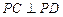 ,
,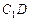 与
与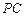 在同一个平面内,所以
在同一个平面内,所以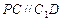 .
.
而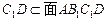 ,所以
,所以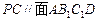 ,所以
,所以 .
.
 ,
,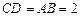 ,
,所以
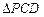 为等腰直角三角形,所以
为等腰直角三角形,所以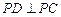 .
. 因为
 是一个长方体,所以
是一个长方体,所以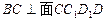 ,而
,而 ,所以
,所以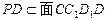 ,所以
,所以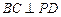 .
. 因为
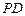 垂直于平面
垂直于平面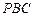 内的两条相交直线
内的两条相交直线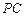 和
和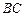 ,
,由线面垂直的判定定理,可得
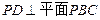
(Ⅱ)解:当
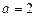 时,
时, .
. 当
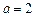 时,四边形
时,四边形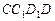 是一个正方形,所以
是一个正方形,所以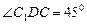 ,而
,而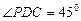 ,
,所以
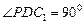 ,所以
,所以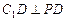 .
. 而
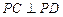 ,
,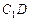 与
与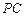 在同一个平面内,所以
在同一个平面内,所以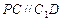 .
. 而
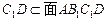 ,所以
,所以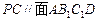 ,所以
,所以 .
. 
练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案
相关题目
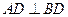 ,且E,F分别是AB,BD的中点,
,且E,F分别是AB,BD的中点,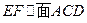 ;
;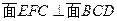 。
。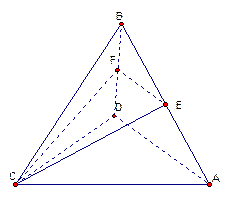
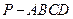 中,
中,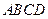 是平行四边形,
是平行四边形,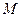 ,
,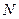 分别是
分别是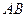 ,
,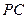 的中点.
的中点.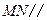 平面
平面 .
.
 的底面边长和各侧棱长都是13,
的底面边长和各侧棱长都是13,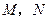 分别是
分别是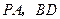 上的点且
上的点且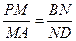 .求证:直线
.求证:直线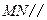 平面
平面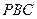

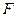 为
为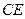 上的点,且
上的点,且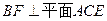 ,
,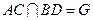 .
.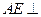 平面
平面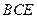 ;
;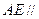 平面
平面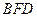 ;
;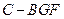 的体积
的体积