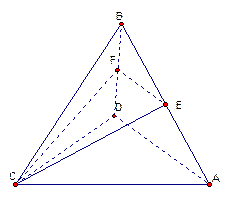
题目内容
(1)求证:AE
 BE;
BE;(2)求三棱锥D—AEC的体积;
(3)求二面角A—CD—E的余弦值.
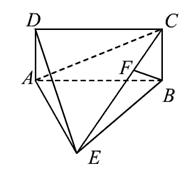
(2)4/3 (3)
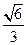
(1)证明: ABCD是矩形
ABCD是矩形
 BC
BC AB
AB
 平面EAB
平面EAB 平面ABCD,平面EAB
平面ABCD,平面EAB 平面ABCD=AB,BC
平面ABCD=AB,BC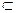 平面ABCD
平面ABCD
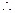 BC
BC 平面EAB
平面EAB
 EA
EA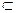 平面EAB
平面EAB
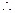 BC
BC EA ……2分
EA ……2分
 BF
BF 平面ACE,EA
平面ACE,EA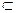 平面ACE
平面ACE
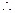 BF
BF EA ……3分
EA ……3分
 BC
BC 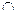 BF=B,BC
BF=B,BC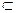 平面EBC,BF
平面EBC,BF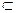 平面EBC
平面EBC
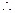 EA
EA 平面EBC
平面EBC
 BE
BE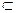 平面EBC
平面EBC
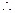 EA
EA BE ……5分
BE ……5分
(2) EA
EA BE
BE
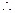 AB=
AB=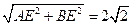
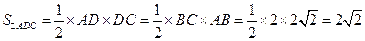 ……6分
……6分
设O为AB的中点,连结EO,
 AE=EB=2
AE=EB=2
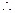 EO
EO AB
AB
 平面EAB
平面EAB 平面ABCD
平面ABCD
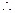 EO
EO 平面ABCD,即EO为三棱锥E—ADC的高,且EO=
平面ABCD,即EO为三棱锥E—ADC的高,且EO=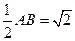 ……8分
……8分
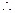
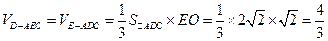 ……9分
……9分
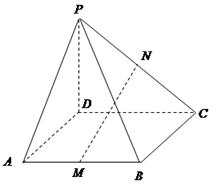
 (3)以O为原点,分别以OE、OB所在直线为
(3)以O为原点,分别以OE、OB所在直线为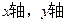 ,如图建立空间直角坐标系,则
,如图建立空间直角坐标系,则 ,
,
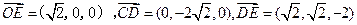
……10分
由(2)知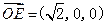 是平面ACD的一个法向量,
是平面ACD的一个法向量,
设平面ECD的法向量为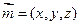 ,则
,则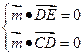
即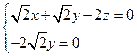
令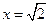 ,则
,则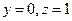 ,所以
,所以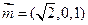 ……12分
……12分
设二面角A—CD—E的平面角的大小为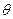 ,由图得
,由图得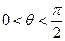 ,则
,则
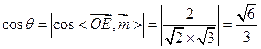 ……13分
……13分
所以二面角A—CD—E的余弦值为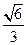 ……14分
……14分
若(1)、(2)问都用向量做,按步骤给分就可以
 ABCD是矩形
ABCD是矩形 BC
BC AB
AB 平面EAB
平面EAB 平面ABCD,平面EAB
平面ABCD,平面EAB 平面ABCD=AB,BC
平面ABCD=AB,BC 平面ABCD
平面ABCD BC
BC 平面EAB
平面EAB  EA
EA 平面EAB
平面EAB BC
BC EA ……2分
EA ……2分 BF
BF 平面ACE,EA
平面ACE,EA 平面ACE
平面ACE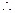 BF
BF EA ……3分
EA ……3分 BC
BC 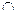 BF=B,BC
BF=B,BC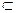 平面EBC,BF
平面EBC,BF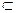 平面EBC
平面EBC EA
EA 平面EBC
平面EBC  BE
BE 平面EBC
平面EBC EA
EA BE ……5分
BE ……5分(2)
 EA
EA BE
BE AB=
AB=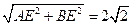
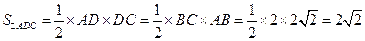 ……6分
……6分设O为AB的中点,连结EO,
 AE=EB=2
AE=EB=2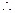 EO
EO AB
AB 平面EAB
平面EAB 平面ABCD
平面ABCD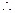 EO
EO 平面ABCD,即EO为三棱锥E—ADC的高,且EO=
平面ABCD,即EO为三棱锥E—ADC的高,且EO=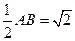 ……8分
……8分
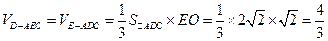 ……9分
……9分 (3)以O为原点,分别以OE、OB所在直线为
(3)以O为原点,分别以OE、OB所在直线为 ,如图建立空间直角坐标系,则
,如图建立空间直角坐标系,则 ,
,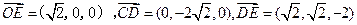
……10分
由(2)知
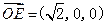 是平面ACD的一个法向量,
是平面ACD的一个法向量,设平面ECD的法向量为
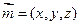 ,则
,则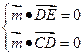
即
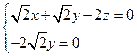
令
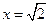 ,则
,则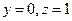 ,所以
,所以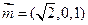 ……12分
……12分设二面角A—CD—E的平面角的大小为
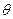 ,由图得
,由图得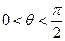 ,则
,则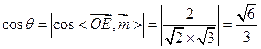 ……13分
……13分所以二面角A—CD—E的余弦值为
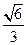 ……14分
……14分若(1)、(2)问都用向量做,按步骤给分就可以

练习册系列答案
相关题目
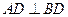 ,且E,F分别是AB,BD的中点,
,且E,F分别是AB,BD的中点,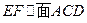 ;
;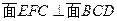 。
。
 中,
中, 是平行四边形,
是平行四边形, ,
,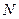 分别是
分别是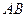 ,
,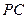 的中点.
的中点.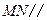 平面
平面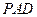 .
.
 交正方形
交正方形 于
于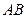 ,
,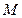 、
、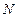 在对角线
在对角线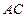 、
、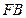 上,且
上,且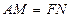 ,求证:
,求证: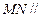 平面
平面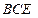 。
。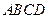
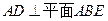
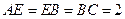

 为
为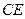 上的点,且
上的点,且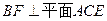 ,
,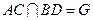 .
.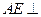 平面
平面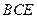 ;
;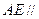 平面
平面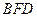 ;
;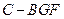 的体积
的体积
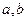 为不重合的两条直线,
为不重合的两条直线,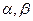 为不重合的两个平面,给出下列命题:
为不重合的两个平面,给出下列命题: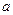 ∥
∥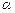 且
且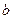 ∥
∥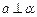 且
且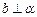 ,则
,则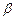 ,则
,则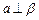 ,则
,则