Question

【题目】三棱锥D﹣ABC及其正视图和侧视图如右图所示，且顶点A，B，C，D均在球O的表面上，则球O的表面积为（ ）
A.32π
B.36π
C.128π
D.144π

Answer 1

【答案】A
【解析】解：由三视图可得：DC⊥平面ABC且底面△ABC为正三角形， 如图所示，取AC中点F，连BF，则BF⊥AC，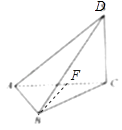

在Rt△BCF中，BF=2，CF=2，BC=4，
在Rt△BCD中，CD=4，所以BD=4 ．
设球心到平面ABC的距离为d，
因为DC⊥平面ABC，且底面△ABC为正三角形，所以d=2，
因为△ABC的外接圆的半径为2，
所以由勾股定理可得R2=d2+22=8，
则该三棱锥外接球的半径R=2 ，
所以三棱锥外接球的表面积是4πR2=32π，
故选A．
【考点精析】通过灵活运用简单空间图形的三视图，掌握画三视图的原则：长对齐、高对齐、宽相等即可以解答此题．