题目内容
【题目】给出下列命题：
存在每个面都是直角三角形的四面体；
若三棱锥的三条侧棱两两垂直，则其三个侧面也两两垂直；
棱台的侧棱延长后交于一点；
用一个平面去截棱锥，棱锥底面和截面之间的部分是棱台；
其中正确命题的个数是
A. 1 B. 2 C. 3 D. 4
【答案】C
【解析】
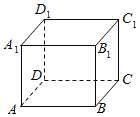
由正方体中四面体
，可判断
；由线面垂直推导面面垂直可判断
；运用棱台的定义可判断
．
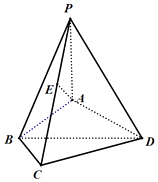
对于，存在每个面都是直角三角形的四面体，如四面体，故正确；
对于，若三棱锥的三条侧棱两两垂直，则其三个侧面也两两垂直，
比如正方体中共顶点的三个相邻平面，故正确；
对于
，由棱台的定义可得棱台的侧棱延长后交于一点，故正确；
对于
，用一个平行于底面的平面去截棱锥，棱锥底面和截面之间的部分是棱台，故错误．
故选：C．
练习册系列答案
相关题目
