题目内容
【题目】如图所示,有一块矩形空地ABCD,AB=2km,BC=4km,根据周边环境及地形实际,当地政府规划在该空地内建一个筝形商业区AEFG,筝形的顶点A,E,F,G为商业区的四个入口,其中入口F在边BC上(不包含顶点),入口E,G分别在边AB,AD上,且满足点A,F恰好关于直线EG对称,矩形内筝形外的区域均为绿化区. 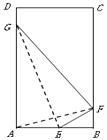
(1)请确定入口F的选址范围;
(2)设商业区的面积为S1 , 绿化区的面积为S2 , 商业区的环境舒适度指数为 ![]() ,则入口F如何选址可使得该商业区的环境舒适度指数最大?
,则入口F如何选址可使得该商业区的环境舒适度指数最大?
【答案】
(1)解:以A为原点,AB所在直线为x轴,建立如图所示平面直角坐标系,
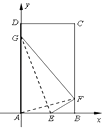
则A(0,0),
设F(2,2a)(0<2a<4),则AF的中点为(1,a),斜率为a,
而EG⊥AF,故EG的斜率为 ![]() ,
,
则EG的方程为 ![]() ,
,
令x=0,得 ![]() ;
;
令y=0,得 ![]() ;
;
由 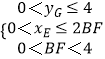 ,得
,得 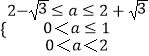 ,
,
∴ ![]() ,
,
即入口F的选址需满足BF的长度范围是 ![]() (单位:km)
(单位:km)
(2)解:因为 ![]() ,
,
故该商业区的环境舒适度指数 ![]() ,
,
所以要使 ![]() 最大,只需S1最小.
最大,只需S1最小.
设 ![]() ,
,
则 ![]() ,
,
令f'(a)=0,得 ![]() 或
或 ![]() (舍),
(舍),
a,f'(a),f(a)的情况如下表:
a | 2﹣ | (2﹣ |
|
| 1 |
f'(a) | ﹣ | 0 | + | ||
f(a) | 减 | 极小 | 增 |
故当 ![]() ,即入口F满足
,即入口F满足 ![]() km时,该商业区的环境舒适度指数最大
km时,该商业区的环境舒适度指数最大
【解析】(1)以A为原点,AB所在直线为x轴,建立如图所示平面直角坐标系,则A(0,0),设F(2,2a)(0<2a<4),则AF的中点为(1,a),斜率为a,EG⊥AF,求出EG的方程,列出不等式即可求出;(2)因为 ![]() ,该商业区的环境舒适度指数
,该商业区的环境舒适度指数 ![]() ,所以要使
,所以要使 ![]() 最大,只需S1最小.转化为求其最小值.
最大,只需S1最小.转化为求其最小值.
【考点精析】认真审题,首先需要了解利用导数研究函数的单调性(一般的,函数的单调性与其导数的正负有如下关系: 在某个区间![]() 内,(1)如果
内,(1)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递增;(2)如果
在这个区间单调递增;(2)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递减).
在这个区间单调递减).

 名校课堂系列答案
名校课堂系列答案