题目内容
(本题12分)已知曲线y=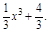
(1)求曲线在x=2处的切线方程;(2)求曲线过点(2,4)的切线方程.
(1)4x-y-4="0." (2)4x-y-4=0或x-y+2=0.
解析试题分析:(1)∵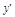 =x2,∴在点P(2,4)处的切线的斜率k=
=x2,∴在点P(2,4)处的切线的斜率k=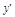 |x=2="4." ……………2分
|x=2="4." ……………2分
∴曲线在点P(2,4)处的切线方程为y-4=4(x-2),即4x-y-4="0." …………………… 4分
(2)设曲线y=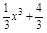 与过点P(2,4)的切线相切于点
与过点P(2,4)的切线相切于点 ,
,
则切线的斜率k=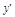 |
| =
= . ……………… 6分
. ……………… 6分
∴切线方程为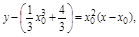 即
即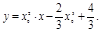 …………………… 8分
…………………… 8分
∵点P(2,4)在切线上,∴4=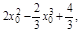
即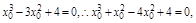 ∴
∴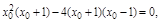
∴(x0+1)(x0-2)2=0,解得x0=-1或x0=2,
故所求的切线方程为4x-y-4=0或x-y+2=0. ……………………12分
考点:本题主要考查导数的几何意义。
点评:易错题,求曲线的切线问题,往往包括两种类型,一是知切点,二是过曲线外的点,后者难度大些。

练习册系列答案
相关题目
 与
与 ,
, ,
, 所围成的平面图形的面积。
所围成的平面图形的面积。
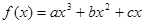 在区间[0,1]上是增函数,在区间
在区间[0,1]上是增函数,在区间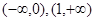 上是减函数,又
上是减函数,又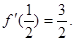
 的解析式;
的解析式;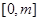 (m>0)上恒有
(m>0)上恒有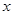 成立,求m的取值范围.
成立,求m的取值范围. .
. ,求
,求 的最小值;
的最小值; ,讨论函数
,讨论函数
 R,对任意的a∈(-l,1),总存在xo∈[1,e],使得不等式ma - (xo)<0成立,求实数m的取值范围;
R,对任意的a∈(-l,1),总存在xo∈[1,e],使得不等式ma - (xo)<0成立,求实数m的取值范围; ∈N*).
∈N*).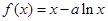 ,
,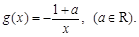
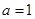 ,求函数
,求函数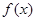 的极值;
的极值; ,求函数
,求函数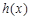 的单调区间;
的单调区间;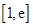 (
( )上存在一点
)上存在一点 ,使得
,使得
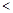
 成立,求
成立,求 的取值范围.
的取值范围. ,
,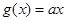 ,
,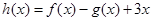 ,其中
,其中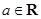 且
且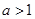 .
. 的导函数
的导函数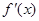 的最小值;
的最小值;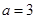 时,求函数
时,求函数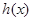 的单调区间及极值;
的单调区间及极值; ,函数
,函数 ,求实数
,求实数 的取值范围.
的取值范围.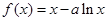 ,
,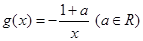 .
.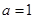 ,求函数
,求函数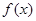 的极值;
的极值;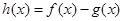 ,求函数
,求函数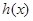 的单调区间;
的单调区间;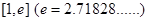 上不存在
上不存在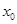 ,使得
,使得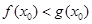 成立,求实数
成立,求实数 的取值范围.
的取值范围. 是实数,函数
是实数,函数 。
。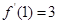 ,求
,求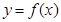 在点
在点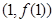 处的切线方程;
处的切线方程; 在区间
在区间 上的最大值。
上的最大值。