题目内容
求由曲线
与
，
，
所围成的平面图形的面积。
1
解析试题分析：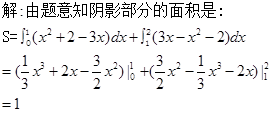
考点：本题主要考查定积分的几何意义。
点评：简单题，分析函数图象，明确所求面积图形特征，利用定积分计算面积。
练习册系列答案
口算题卡加应用题集训系列答案
综合自测系列答案
相关题目
口算题卡加应用题集训系列答案综合自测系列答案题目内容
求由曲线与，，所围成的平面图形的面积。
1
解析试题分析：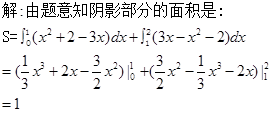
考点：本题主要考查定积分的几何意义。
点评：简单题，分析函数图象，明确所求面积图形特征，利用定积分计算面积。
口算题卡加应用题集训系列答案综合自测系列答案
其中
=0，求
的单调区间；
表示
与
两个数中的最大值，求证：当0≤x≤1时，|
|≤
.
的单调区间与极值；
，使得对任意的
，当
时恒有
成立．若存在，求
，其中
．
有极值，求
的取值范围；
，
恒成立，求
其中
，曲线
在点
处的切线垂直于
轴.
的值；
的极值.
时，求函数
的最值；
(x∈R)在区间[－1，1]上是增函数.
的两个非零实根为x1、x2.试问：是否存在实数m，使得不等式m2+tm+1≥|x1－x2|对任意a∈A及t∈[－1，1]恒成立？若存在，求m的取值范围；若不存在，请说明理由.
，求函数
的极小值；
，试问：在定义域内是否存在三个不同的自变量
使得
的值相等，若存在，请求出
的范围，若不存在，请说明理由？