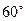题目内容
(本小题满分10分)选修4-1:几何证明选讲
如图,已知 的两条角平分线
的两条角平分线 和
和 相交于H,
相交于H, ,F在
,F在 上,且
上,且 。
。

(Ⅰ)证明:B、D、H、E四点共圆;
(Ⅱ)证明: 平分
平分 。
。
如图,已知
 的两条角平分线
的两条角平分线 和
和 相交于H,
相交于H, ,F在
,F在 上,且
上,且 。
。
(Ⅰ)证明:B、D、H、E四点共圆;
(Ⅱ)证明:
 平分
平分 。
。(Ⅰ)证明见解析。
(Ⅱ)证明见解析。
(Ⅱ)证明见解析。
(Ⅰ)在△ABC中,因为∠B=60°,
所以∠BAC+∠BCA=120°。
因为AD,CE是角平分线,
所以∠HAC+∠HCA=60°,
故∠AHC=120°。
于是∠EHD=∠AHC=120°。
因为∠EBD+∠EHD=180°,
所以B、D、H、E四点共圆。
(Ⅱ)连结BH,则BH为∠ABC的平分线,得∠HBD=30°
由(Ⅰ)知B、D、H、E四点共圆,
所以∠CED=∠HBD=30°。
又∠AHE=∠EBD=60°,由已知可得EF⊥AD,
可得∠CEF=30°。
所以CE平分∠DEF。
所以∠BAC+∠BCA=120°。
因为AD,CE是角平分线,
所以∠HAC+∠HCA=60°,
故∠AHC=120°。
于是∠EHD=∠AHC=120°。
因为∠EBD+∠EHD=180°,
所以B、D、H、E四点共圆。
(Ⅱ)连结BH,则BH为∠ABC的平分线,得∠HBD=30°
由(Ⅰ)知B、D、H、E四点共圆,
所以∠CED=∠HBD=30°。
又∠AHE=∠EBD=60°,由已知可得EF⊥AD,
可得∠CEF=30°。
所以CE平分∠DEF。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 =
= ,
,  =
= ,求
,求 ,
, 及
及 的值
的值

 (a>0,b>0)的两个焦点为F1、F2,若P为其上一点,且|PF1|=2|PF2|,则双曲线离心率的取值范围为( )
(a>0,b>0)的两个焦点为F1、F2,若P为其上一点,且|PF1|=2|PF2|,则双曲线离心率的取值范围为( )
 )
)
 为圆心的圆与
为圆心的圆与 轴交于点
轴交于点 、
、 ,与
,与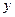 轴交于点
轴交于点 ,其中
,其中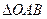 的面积;
的面积;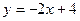 与圆
与圆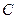 交于点
交于点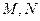 ,若
,若 ,求圆
,求圆 有相同的焦点,且椭圆过点
有相同的焦点,且椭圆过点 ,
, 过点
过点 交椭圆于
交椭圆于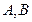 两点,且
两点,且 ,求直线
,求直线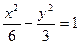 的渐近线与圆
的渐近线与圆 相切,则r=
相切,则r=
 :
: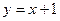 ,则该直线的倾斜角为( )
,则该直线的倾斜角为( )