题目内容
(本题满分14分)设点F（0,2），曲线C上任意一点M（x,y）满足以线段FM为直径的圆与x 轴相切.
（1）求曲线C的方程；
（2）设过点Q（0，－2）的直线l与曲线C交于A,B两点，问|FA|,|AB|,|FB|能否成等差数列？若能，求出直线l的方程；若不能，请说明理由.
（1）求曲线C的方程；
（2）设过点Q（0，－2）的直线l与曲线C交于A,B两点，问|FA|,|AB|,|FB|能否成等差数列？若能，求出直线l的方程；若不能，请说明理由.
（1）设M（x,y）,则由题可知：
化简可得曲线C的方程为：
（2）设
，直线l的方程为：y=kx-2,代入得：
而由题可知：2|AB|=|FA|+|FB|
代入可得：
所以|FA|,|AB|,|FB|能成等差数列，此时l的方程为：
化简可得曲线C的方程为：
（2）设
，直线l的方程为：y=kx-2,代入得：而由题可知：2|AB|=|FA|+|FB|
代入可得：
所以|FA|,|AB|,|FB|能成等差数列，此时l的方程为：
略
练习册系列答案
新题型全程检测期末冲刺100分系列答案
相关题目
的两条角平分线
和
相交于H，
，F在
上，且
。
。
的极坐标方程为
，直线
的参数方程是：
.
，再向左平移1个单位，得到曲线曲线
，求曲线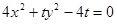
的虚轴长等于( ) 
的圆心C，且与直线
垂直的直线方程是 （ ）
为椭圆
的左、右焦点，
是椭圆上一点。
的最大值；
且
的面积为
，求
的值；
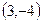与圆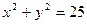
相切的直线方程是 ．
=1的左焦点F引圆x2 + y2 = 3的切线FP交双曲线右支于点P，T为切点，M为线段FP的中点，O为坐标原点，则| MO | – | MT | 等于 。