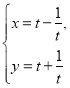题目内容
【题目】已知函数![]() .
.
(1)求![]() 的单调递增区间;
的单调递增区间;
(2)求证:曲线![]() 在区间
在区间![]() 上有且只有一条斜率为2的切线.
上有且只有一条斜率为2的切线.
【答案】(1)![]() ,
,![]() (2)见解析
(2)见解析
【解析】
(1)根据函数解析式,求得导函数![]() ,令
,令![]() 即可求得
即可求得![]() 的单调递增区间;
的单调递增区间;
(2)曲线![]() 在区间
在区间![]() 上有且只有一条斜率为2的切线,等价于在区间
上有且只有一条斜率为2的切线,等价于在区间![]() 上方程
上方程![]() 有唯一解,构造函数
有唯一解,构造函数![]() ,求得导函数
,求得导函数![]() ,并判断
,并判断![]() 的符号,确定
的符号,确定![]() 的单调性与极值,从而判断出
的单调性与极值,从而判断出![]() 在
在![]() 上存在唯一一个零点,即可证明结论.
上存在唯一一个零点,即可证明结论.
(1)函数![]() ,
,![]() ,
,
则![]() ,
,
令![]() 得
得![]() ,
,![]() ,
,
∴![]() 单调递增区间为
单调递增区间为![]() ,
,![]()
(2)原命题等价于:在区间![]() 上,方程
上,方程![]() 有唯一解,
有唯一解,
设![]() ,
,![]()
则![]()
此时,![]() ,
,![]() ,
,![]() 变化情况如下:
变化情况如下:
|
|
|
|
|
| 0 |
|
|
| 极大值 |
|
此时,![]() 在
在![]() 上单调递增,且
上单调递增,且![]() ,
,![]() ,
,
![]() 在
在![]() 上单调递减,且
上单调递减,且![]() ,
,
∴![]() 在
在![]() 上存在唯一一个根,
上存在唯一一个根,
![]() 在
在![]() 上存在唯一一个零点,
上存在唯一一个零点,
∴曲线![]() 在区间
在区间![]() 上有且仅有一条斜率为2的切线.
上有且仅有一条斜率为2的切线.

练习册系列答案
 同步学典一课多练系列答案
同步学典一课多练系列答案 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案
相关题目