题目内容
【题目】在直三棱柱![]() 中,
中,![]() ,
,![]() ,点
,点![]() ,
,![]() ,
,![]() 分别是棱
分别是棱![]() ,
,![]() ,
,![]() 的中点.
的中点.
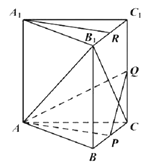
(1)求证:![]() 平面
平面![]() ;
;
(2)求证:直线![]() 平面
平面![]() .
.
【答案】(1)详见解析;(2)详见解析.
【解析】
(1)通过证明四边形![]() 是平行四边形,推出
是平行四边形,推出![]() ,然后利用直线与平面平行的判定定理证明
,然后利用直线与平面平行的判定定理证明![]() 平面
平面![]() .
.
(2)说明![]() ,证明
,证明![]() ,利用直线与平面垂直的判定定理证明
,利用直线与平面垂直的判定定理证明![]() 平面
平面![]() .
.
(1)在直三棱柱![]() 中,
中,![]() 且
且![]() ,
,
因点![]() ,
,![]() 分别是棱
分别是棱![]() ,
,![]() 的中点,所以
的中点,所以![]() 且
且![]() ,
,
所以四边形![]() 是平行四边形,即
是平行四边形,即![]() 且
且![]() ,
,
又![]() 且
且![]() ,所以
,所以![]() 且
且![]() ,
,
即四边形![]() 是平行四边形,所以
是平行四边形,所以![]() ,
,
又![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() .
.
(2)因为直三棱柱![]() ,所以四边形
,所以四边形![]() 是平行四边形,
是平行四边形,
又因![]() ,
,
所以四边形![]() 是菱形,所以
是菱形,所以![]() ,
,
又点![]() ,
,![]() 分别是棱
分别是棱![]() ,
,![]() 的中点,
的中点,
即![]() ,所以
,所以![]() .
.
因为![]() ,点
,点![]() 是棱
是棱![]() 的中点,所以
的中点,所以![]() ,
,
由直三棱柱![]() ,知
,知![]() 底面
底面![]() ,即
,即![]() ,
,
又![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,且
,且![]() ,
,
所以![]() 平面
平面![]() ,
,
又![]() 平面
平面![]() ,则
,则![]() ,
,
又![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,且
,且![]() ,
,
所以![]() 平面
平面![]() .
.

 名校课堂系列答案
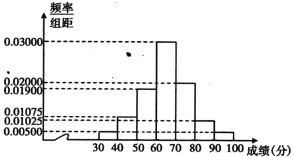
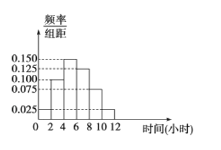
名校课堂系列答案【题目】某中学共有1000人,其中男生700人,女生300人,为了了解该校学生每周平均体育锻炼时间的情况以及经常进行体育锻炼的学生是否与性别有关(经常进行体育锻炼是指:周平均体育锻炼时间不少于4小时),现在用分层抽样的方法从中收集200位学生每周平均体育锻炼时间的样本数据(单位:小时),其频率分布直方图如图.已知在样本数据中,有40位女生的每周平均体育锻炼时间超过4小时,根据独立性检验原理( )
附: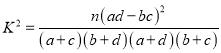 ,其中
,其中![]() .
.
| 0.10 | 0.05 | 0.01 | 0.005 |
| 2.706 | 3.841 | 6.635 | 7.879 |
A.有95%的把握认为“该校学生每周平均体育锻炼时间与性别无关”
B.有90%的把握认为“该校学生每周平均体育锻炼时间与性别有关”
C.有90%的把握认为“该校学生每周平均体育锻炼时间与性别无关”
D.有95%的把握认为“该校学生每周平均体育锻炼时间与性别有关”
【题目】某省从2021年开始,高考采用取消文理分科,实行“![]() ”的模式,其中的“1”表示每位学生必须从物理、历史中选择一个科目且只能选择一个科目.某校高一年级有2000名学生(其中女生900人).该校为了解高一年级学生对“1”的选课情况,采用分层抽样的方法抽取了200名学生进行问卷调查,下表是根据调查结果得到的
”的模式,其中的“1”表示每位学生必须从物理、历史中选择一个科目且只能选择一个科目.某校高一年级有2000名学生(其中女生900人).该校为了解高一年级学生对“1”的选课情况,采用分层抽样的方法抽取了200名学生进行问卷调查,下表是根据调查结果得到的![]() 列联表.
列联表.
性别 | 选择物理 | 选择历史 | 总计 |
男生 | ________ | 50 |
|
女生 | 30 | ________ |
|
总计 | ________ | ________ | 200 |
(1)求![]() ,
,![]() 的值;
的值;
(2)请你依据该列联表判断是否有99.5%的把握认为选择科目与性别有关?说明你的理由.
| 0.100 | 0.050 | 0.025 | 0.010 | 0.005 | 0.001/span> |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
附: ,其中
,其中![]() .
.