题目内容
【题目】如图,在三棱柱![]() 中,
中,![]() 平面
平面![]() ,
,![]() ,
,![]() ,
,![]() 分别是
分别是![]() ,
,![]() ,
,![]() 的中点,点
的中点,点![]() 在线段
在线段![]() 上,
上,![]() .
.

(1)求证:![]() 平面
平面![]() ;
;
(2)若平面![]() 平面
平面![]() ,
,![]() ,
,![]() ,求点
,求点![]() 到平面
到平面![]() 的距离.
的距离.
【答案】(1)证明见解析;(2)![]()
【解析】
(1)由![]() ,
,![]() 分别是
分别是![]() ,
,![]() 的中点,可得
的中点,可得![]() ,再由线面平行的判定定理即可证出;
,再由线面平行的判定定理即可证出;
(2)根据平面![]() 平面
平面![]() ,可得点
,可得点![]() 是线段
是线段![]() 上靠近
上靠近![]() 的四等分点,从而可求得
的四等分点,从而可求得![]() ,利用等体积法即可求出点
,利用等体积法即可求出点![]() 到平面
到平面![]() 的距离.
的距离.
(1)因为在![]() 中,
中,![]() ,
,![]() 分别是
分别是![]() ,
,![]() 的中点,
的中点,
所以![]() ,又
,又![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() .
.
(2)设点![]() 到平面
到平面![]() 的距离为
的距离为![]() ,点
,点![]() 到平面
到平面![]() 的距离为
的距离为![]() ,则
,则![]()
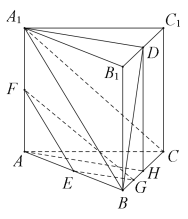
取![]() 的中点
的中点![]() 连结
连结![]() ,
,![]() ,则
,则![]() ,
,
又![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() ,
,
又平面![]() 平面
平面![]() ,而
,而![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() ,又
,又![]() 平面
平面![]() ,所以
,所以![]() ,
,
又![]() 为
为![]() 的中点,所以
的中点,所以![]() 为
为![]() 的中点,
的中点,
所以点![]() 是线段
是线段![]() 上靠近
上靠近![]() 的四等分点,所以
的四等分点,所以![]() ,
,
所以![]() ,
,![]() ,
,
在![]() 中,由余弦定理,得
中,由余弦定理,得
![]() ,
,
所以![]() ,
,
在![]() 中,由余弦定理,得
中,由余弦定理,得
![]() ,
,
所以![]() ,
,
所以![]() ,
,
解得![]() ,即点
,即点![]() 到平面
到平面![]() 的距离
的距离![]() .
.

 智慧课堂密卷100分单元过关检测系列答案
智慧课堂密卷100分单元过关检测系列答案 单元期中期末卷系列答案
单元期中期末卷系列答案【题目】随着经济的不断发展和人们消费观念的不断提升,越来越多的人日益喜爱旅游观光.某人想在2019年5月到某景区![]() 旅游观光,为了避开旅游高峰拥挤,方便出行,他收集了最近5个月该景区的观光人数数据见下表:
旅游观光,为了避开旅游高峰拥挤,方便出行,他收集了最近5个月该景区的观光人数数据见下表:
月份 | 2018.12 | 2019.1 | 2019.2 | 2019.3 | 2019.4 |
月份编号 | 1 | 2 | 3 | 4 | 5 |
旅游观光人数 | 0.5 | 0.6 | 1 | 1.4 | 1.7 |
(1)由收集数据的散点图发现,可用线性回归模型拟合旅游观光人数少![]() (百万人)与月份编号
(百万人)与月份编号![]() 之间的相关关系,请用最小二乘法求
之间的相关关系,请用最小二乘法求![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ,并预测2019年5月景区
,并预测2019年5月景区![]() 的旅游观光人数.
的旅游观光人数.
(2)当地旅游局为了预测景区![]() 给当地的财政带来的收入状况,从2019年4月的旅游观光人群中随机抽取了200人,并对他们旅游观光过程中的开支情况进行了调查,得到如下频率分布表:
给当地的财政带来的收入状况,从2019年4月的旅游观光人群中随机抽取了200人,并对他们旅游观光过程中的开支情况进行了调查,得到如下频率分布表:
开支金额(千元) |
|
|
|
|
|
|
|
频数 | 10 | 30 | 40 | 60 | 30 | 20 | 10 |
若采用分层抽样的方法从开支金额低于4千元的游客中抽取8人,再在这8人中抽取3人,记这3人中开支金额低于3千元的人数为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
(参考公式:![]() ,其中
,其中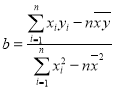 ,
,![]() .)
.)

