题目内容
【题目】如图,在多面体![]() 中,平面
中,平面![]() 平面
平面![]() ,
,![]() ∥
∥![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
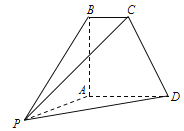
(1)求多面体![]() 的体积;
的体积;
(2)已知![]() 是棱
是棱![]() 的中点,在棱
的中点,在棱![]() 是否存在点
是否存在点![]() 使得
使得![]() ∥
∥![]() ,若存在,请确定点
,若存在,请确定点![]() 的位置;若不存在,请说明理由.
的位置;若不存在,请说明理由.
【答案】(1)![]() (2)不存在.见解析
(2)不存在.见解析
【解析】
(1)作![]() 交
交![]() 的延长线于
的延长线于![]() ,先证明
,先证明![]() 为点
为点![]() 到平面
到平面![]() 的距离,求出
的距离,求出![]() 的长度,再利用三棱锥的体积公式求多面体
的长度,再利用三棱锥的体积公式求多面体![]() 的体积;
的体积;
(2)假设棱![]() 上存在点
上存在点![]() ,使得
,使得![]() ∥
∥![]() .再证明
.再证明![]() 是
是![]() 与
与![]() 的交点
的交点![]() ,即
,即![]() 就是
就是![]() ,而
,而![]() 与
与![]() 相交,这与
相交,这与![]() ∥
∥![]() 相矛盾.即得证.
相矛盾.即得证.
解:(1)如图,

作![]() 交
交![]() 的延长线于
的延长线于![]() ,
,
因为平面![]() 平面
平面![]() ,
,
平面![]() 平面
平面![]() ,且
,且![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() ,所以
,所以![]() 为点
为点![]() 到平面
到平面![]() 的距离.
的距离.
因为![]() ,
,![]() ,所以
,所以![]() ,
,
又![]() ,
,
所以![]() .
.
(2)假设棱![]() 上存在点
上存在点![]() ,使得
,使得![]() ∥
∥![]() .
.

连接![]() ,取
,取![]() 的中点
的中点![]() ,
,
在△![]() 中,因为
中,因为![]() 分别为
分别为![]() 的中点,
的中点,
所以![]() ∥
∥![]() .
.
因为过直线外一点有且只有一条直线和已知直线平行,
所以![]() 与
与![]() 重合.
重合.
因为点![]() 在线段
在线段![]() 上,
上,
所以![]() ,
,
又![]() ,
,
所以![]() 是
是![]() 与
与![]() 的交点
的交点![]() ,即
,即![]() 就是
就是![]() ,
,
而![]() 与
与![]() 相交,
相交,
这与![]() ∥
∥![]() 相矛盾,
相矛盾,
所以假设不成立,
故棱![]() 上不存在点
上不存在点![]() 使得
使得![]() ∥
∥![]() .
.

 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案【题目】(在花卉进行硬枝扦插过程中,常需要用生根粉调节植物根系生长.现有20株使用了生根粉的花卉,在对最终“花卉存活”和“花卉死亡”进行统计的同时,也对在使用生根粉2个小时后的生根量进行了统计,这20株花卉生根量如下表所示,其中生根量在6根以下的视为“不足量”,大于等于6根为“足量”.现对该20株花卉样本进行统计,其中“花卉存活”的13株.已知“花卉存活”但生根量“不足量”的植株共1株.
编号 | 01 | 02 | 03 | 04 | 05 | 06 | 07 | 08 | 09 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
生根量 | 6 | 8 | 3 | 8 | 9 | 5 | 6 | 6 | 2 | 7 | 7 | 5 | 9 | 6 | 7 | 8 | 8 | 4 | 6 | 9 |
(1)完成![]() 列联表,并判断是否可以在犯错误概率不超过1%的前提下,认为“花卉的存活”与“生根足量”有关?
列联表,并判断是否可以在犯错误概率不超过1%的前提下,认为“花卉的存活”与“生根足量”有关?
生根足量 | 生根不足量 | 总计 | |
花卉存活 | |||
花卉死亡 | |||
总计 | 20 |
(2)若在该样本“生根不足量”的植株中随机抽取3株,求这3株中恰有1株“花卉存活”的概率.
参考数据:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
独立性检验中的 ,其中
,其中![]() .
.
【题目】新生儿某疾病要接种三次疫苗免疫(即0、1、6月龄),假设每次接种之间互不影响,每人每次接种成功的概率相等为了解新生儿该疾病疫苗接种剂量与接种成功之间的关系,现进行了两种接种方案的临床试验:10μg/次剂量组与20μg/次剂量组,试验结果如下:
接种成功 | 接种不成功 | 总计(人) | |
10μg/次剂量组 | 900 | 100 | 1000 |
20μg/次剂量组 | 973 | 27 | 1000 |
总计(人) | 1873 | 127 | 2000 |
(1)根据数据说明哪种方案接种效果好?并判断能否有99.9%的把握认为该疾病疫苗接种成功与两种接种方案有关?
(2)以频率代替概率,若选用接种效果好的方案,参与该试验的1000人的成功人数比此剂量只接种一次的成功人数平均提高多少人.
参考公式: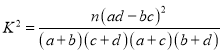 ,其中
,其中![]()
参考附表:
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |