题目内容
(本题满分12分)
已知数列 为公差不为
为公差不为 的等差数列,
的等差数列, 为前
为前 项和,
项和, 和
和 的等差中项为
的等差中项为 ,且
,且 .令
.令 数列
数列 的前
的前 项和为
项和为 .
.
(Ⅰ)求 及
及 ;
;
(Ⅱ)是否存在正整数 成等比数列?若存在,求出所有的
成等比数列?若存在,求出所有的 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
已知数列
 为公差不为
为公差不为 的等差数列,
的等差数列, 为前
为前 项和,
项和, 和
和 的等差中项为
的等差中项为 ,且
,且 .令
.令 数列
数列 的前
的前 项和为
项和为 .
.(Ⅰ)求
 及
及 ;
;(Ⅱ)是否存在正整数
 成等比数列?若存在,求出所有的
成等比数列?若存在,求出所有的 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.(Ⅰ) ,
, 
(Ⅱ)当 可以使
可以使 成等比数列.
成等比数列.
 ,
, 
(Ⅱ)当
 可以使
可以使 成等比数列.
成等比数列.
试题分析:(Ⅰ)因为
 为等差数列,设公差为
为等差数列,设公差为 ,则由题意得
,则由题意得整理得

所以
 ……………3分
……………3分由

所以
 ……………5分
……………5分(Ⅱ)假设存在
由(Ⅰ)知,
 ,所以
,所以
若
 成等比,则有
成等比,则有 ………8分
………8分 ,。。。。。(1)
,。。。。。(1)因为
 ,所以
,所以 ,……………10分
,……………10分因为
 ,当
,当 时,带入(1)式,得
时,带入(1)式,得 ;
;综上,当
 可以使
可以使 成等比数列.……………12分
成等比数列.……………12分点评:高考中中的数列解答题考查的的热点为求数列的通项公式、等差(比)数列的性质及数列的求和问题.因此在高考复习的后期,要特别注意加强对由递推公式求通项公式、求有规律的非等差(比)数列的前n项和等的专项训练.

练习册系列答案
相关题目
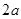 ,1,
,1,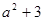 按某种顺序排列成等差数列.
按某种顺序排列成等差数列.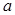 的值;
的值;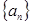 的首项、公差都为
的首项、公差都为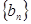 的首项、公比也都为
的首项、公比也都为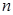 项和分别
项和分别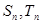 ,且
,且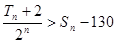 ,求满足条件的正整数
,求满足条件的正整数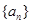 是公比
是公比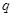 大于1的等比数列,
大于1的等比数列,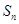 为数列
为数列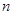 项和,已知
项和,已知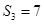 ,且
,且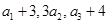 构成等差数列.
构成等差数列.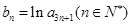 ,求数列
,求数列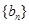 的前
的前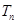 .
.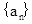 满足:
满足: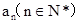 是整数,且
是整数,且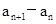 是关于x的方程
是关于x的方程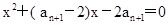 的根.
的根.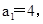 且n≥2时,
且n≥2时,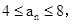 求数列{an}的前100项和S100;
求数列{an}的前100项和S100;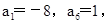 且
且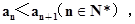 求数列
求数列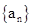 的通项公式.
的通项公式. }满足
}满足 ,且
,且 ,则
,则 的值是( )
的值是( )

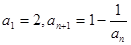 ,则a2007的值 ( )
,则a2007的值 ( )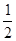
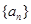 是等差数列,首项公差
是等差数列,首项公差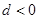 ,
,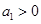 ,且
,且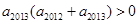 ,则使数列
,则使数列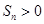 成立的最大自然数n是 ( )
成立的最大自然数n是 ( )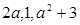 按某种顺序排列成等差数列。
按某种顺序排列成等差数列。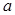 的值;
的值;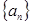 的首项、公差都为
的首项、公差都为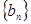 的首项、公比也都为
的首项、公比也都为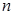 项和分别为
项和分别为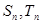 ,且
,且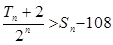 ,求满足条件的正整数
,求满足条件的正整数