题目内容
设a为实数, 函数f(x)=x3-x2-x+a.
(1)求f(x)的极值;
(2)若曲线y=f(x)与x轴仅有一个交点, 求a的取值范围.
(1)求f(x)的极值;
(2)若曲线y=f(x)与x轴仅有一个交点, 求a的取值范围.
(1)f(x)的极大值是f(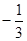 )=
)=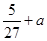 ,极小值是f(1)=a-1.
,极小值是f(1)=a-1.
(2)当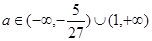 时,曲线y=f(x)与x轴仅有一个交点.
时,曲线y=f(x)与x轴仅有一个交点.
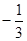 )=
)=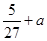 ,极小值是f(1)=a-1.
,极小值是f(1)=a-1.(2)当
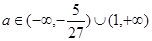 时,曲线y=f(x)与x轴仅有一个交点.
时,曲线y=f(x)与x轴仅有一个交点. 本试题主要是考查了导数在研究函数中的运用。
(1)因为a为实数, 函数f(x)=x3-x2-x+a.求解导数,结合导数的符号判定单调性得到
f(x)的极值;
(2)因为曲线y=f(x)与x轴仅有一个交点, 由此可知x取足够大的正数时有f(x)>0, x取足够小的负数时有f(x)<0.
所以曲线y=f(x)与x轴至少有一个交点,结合导数的思想判定得到。
(1)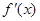 =3x2-2x-1.若
=3x2-2x-1.若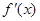 =0,则x=-
=0,则x=-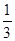 或x=1 ………… 2分
或x=1 ………… 2分
当x变化时,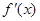 、f(x)的变化情况如下表:
、f(x)的变化情况如下表:
…………4分
所以f(x)的极大值是f(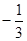 )=
)=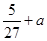 ,极小值是f(1)=a-1.………… 6分
,极小值是f(1)=a-1.………… 6分
(2)函数f(x)=x3-x2-x+a=(x-1)2(x+1)+a-1.
由此可知x取足够大的正数时有f(x)>0, x取足够小的负数时有f(x)<0.
所以曲线y=f(x)与x轴至少有一个交点. …………8分
结合f(x)的单调性可知,
当f(x)的极大值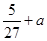 <0,即a
<0,即a
 时,它的极小值也小于0.
时,它的极小值也小于0.
因此曲线y=f(x)与x轴仅有一个交点,它在(1,+ )上.
)上.
当f(x)的极小值a-1>0,即a
 时,它的极大值也大于0.
时,它的极大值也大于0.
因此曲线y=f(x)与x轴仅有一个交点,它在(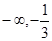 )上.
)上.
所以当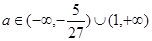 时,曲线y=f(x)与x轴仅有一个交点.…… 12分
时,曲线y=f(x)与x轴仅有一个交点.…… 12分
(1)因为a为实数, 函数f(x)=x3-x2-x+a.求解导数,结合导数的符号判定单调性得到
f(x)的极值;
(2)因为曲线y=f(x)与x轴仅有一个交点, 由此可知x取足够大的正数时有f(x)>0, x取足够小的负数时有f(x)<0.
所以曲线y=f(x)与x轴至少有一个交点,结合导数的思想判定得到。
(1)
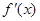 =3x2-2x-1.若
=3x2-2x-1.若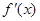 =0,则x=-
=0,则x=-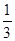 或x=1 ………… 2分
或x=1 ………… 2分当x变化时,
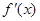 、f(x)的变化情况如下表:
、f(x)的变化情况如下表: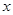 |  | 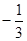 | 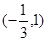 | 1 |  |
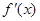 | + | 0 | - | 0 | + |
| f(x) |   | 极大值 |   | 极小值 |  |
…………4分
所以f(x)的极大值是f(
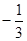 )=
)=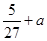 ,极小值是f(1)=a-1.………… 6分
,极小值是f(1)=a-1.………… 6分(2)函数f(x)=x3-x2-x+a=(x-1)2(x+1)+a-1.
由此可知x取足够大的正数时有f(x)>0, x取足够小的负数时有f(x)<0.
所以曲线y=f(x)与x轴至少有一个交点. …………8分
结合f(x)的单调性可知,
当f(x)的极大值
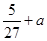 <0,即a
<0,即a
 时,它的极小值也小于0.
时,它的极小值也小于0.因此曲线y=f(x)与x轴仅有一个交点,它在(1,+
 )上.
)上.当f(x)的极小值a-1>0,即a

 时,它的极大值也大于0.
时,它的极大值也大于0.因此曲线y=f(x)与x轴仅有一个交点,它在(
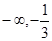 )上.
)上.所以当
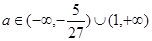 时,曲线y=f(x)与x轴仅有一个交点.…… 12分
时,曲线y=f(x)与x轴仅有一个交点.…… 12分
练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
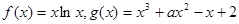
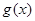 的单调递减区间为
的单调递减区间为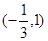 ,求函数
,求函数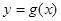 的图像在点
的图像在点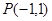 处的切线方程;
处的切线方程;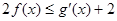 恒成立,求实数
恒成立,求实数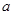 的取值范围.
的取值范围.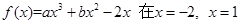 处取得极值。(1)求函数
处取得极值。(1)求函数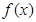 的解析式;
的解析式; ,其中
,其中 。
。 时,判断函数
时,判断函数 在定义域上的单调性;
在定义域上的单调性; ,不等式
,不等式 成立。
成立。 ,且其导函数
,且其导函数 的图像过原点.
的图像过原点. 时,求函数
时,求函数 的图像在
的图像在 处的切线方程;
处的切线方程; ,使得
,使得 ,求
,求 的最大值;
的最大值;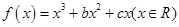 ,已知
,已知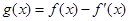 是奇函数。
是奇函数。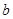 、
、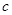 的值。
的值。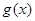 的单调区间与极值。
的单调区间与极值。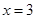 是函数
是函数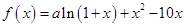 的一个极值点.
的一个极值点.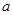 ;(Ⅱ)求函数
;(Ⅱ)求函数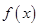 的单调区间;
的单调区间;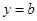 与函数
与函数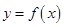 的图象有3个交点,求
的图象有3个交点,求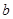 的取值范围.
的取值范围.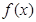 ,若满足
,若满足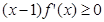 ,则必有( )
,则必有( )
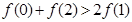
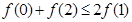 D.
D. 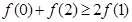
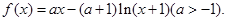
 的单调区间;
的单调区间;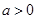 时,设
时,设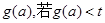 恒成立,求实数t的取值范围.
恒成立,求实数t的取值范围.