题目内容
设函数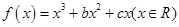 ,已知
,已知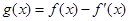 是奇函数。
是奇函数。
(Ⅰ)求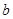 、
、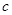 的值。
的值。
(Ⅱ)求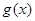 的单调区间与极值。
的单调区间与极值。
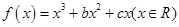 ,已知
,已知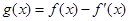 是奇函数。
是奇函数。(Ⅰ)求
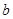 、
、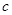 的值。
的值。(Ⅱ)求
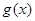 的单调区间与极值。
的单调区间与极值。(Ⅰ)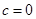 ,
, 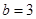 ;(Ⅱ)
;(Ⅱ) 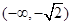 和
和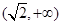 是函数
是函数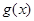 是单调递增区间;
是单调递增区间;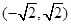 是函数
是函数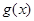 是单调递减区间;
是单调递减区间;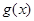 在
在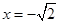 时,取得极大值,极大值为
时,取得极大值,极大值为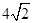 ,
,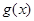 在
在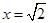 时,取得极小值,极小值为
时,取得极小值,极小值为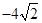 。
。
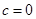 ,
, 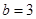 ;(Ⅱ)
;(Ⅱ) 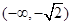 和
和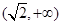 是函数
是函数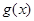 是单调递增区间;
是单调递增区间;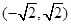 是函数
是函数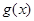 是单调递减区间;
是单调递减区间;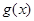 在
在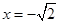 时,取得极大值,极大值为
时,取得极大值,极大值为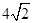 ,
,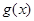 在
在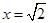 时,取得极小值,极小值为
时,取得极小值,极小值为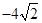 。
。本试题主要是考查了函数的奇偶性和函数的单调性和极值的运用。
(1)利用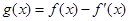 是奇函数可知参数c=0,然后结合函数的定义得到b=3.
是奇函数可知参数c=0,然后结合函数的定义得到b=3.
(2)由(Ⅰ)知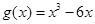 ,从而
,从而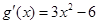 ,由此可知,
,由此可知,
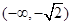 和
和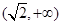 是函数
是函数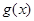 是单调递增区间;
是单调递增区间;
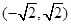 是函数
是函数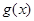 是单调递减区间;从而得到极值
是单调递减区间;从而得到极值
(1)利用
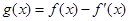 是奇函数可知参数c=0,然后结合函数的定义得到b=3.
是奇函数可知参数c=0,然后结合函数的定义得到b=3.(2)由(Ⅰ)知
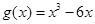 ,从而
,从而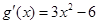 ,由此可知,
,由此可知,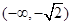 和
和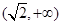 是函数
是函数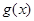 是单调递增区间;
是单调递增区间;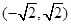 是函数
是函数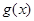 是单调递减区间;从而得到极值
是单调递减区间;从而得到极值
练习册系列答案
 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案
相关题目
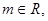 函数
函数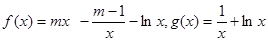
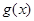 的最小值;
的最小值; 在
在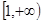 上为单调增函数,求实数
上为单调增函数,求实数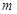 的取值范围;
的取值范围;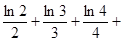 …
…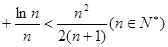 .
.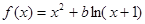 ,其中
,其中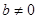
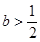 时,判断函数
时,判断函数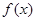 在定义域上的单调性;
在定义域上的单调性;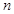 ,不等式
,不等式 都成立。
都成立。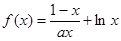 .
. 在
在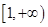 上是增函数,求正实数
上是增函数,求正实数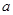 的取值范围;
的取值范围;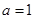 时,求函数
时,求函数 上的最大值和最小值;
上的最大值和最小值; 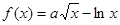
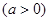
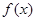 在
在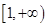 上递增,求
上递增,求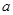 的取值范围;
的取值范围;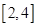 上的存在单调递减区间 ,求
上的存在单调递减区间 ,求 的单调递减区间是
的单调递减区间是



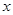 ,有
,有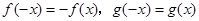 ,且
,且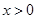 时,
时,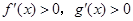 ,则
,则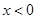 时( )
时( )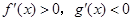
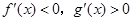
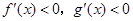
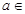 R,函数
R,函数 (x∈R).
(x∈R). 时,求函数f(x)的单调递增区间;
时,求函数f(x)的单调递增区间; 的取值范围;若不能,请说明理由;
的取值范围;若不能,请说明理由; 上单调递增,求
上单调递增,求