题目内容
(本小题满分12分)
设函数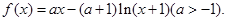
(Ⅰ)求 的单调区间;
的单调区间;
(Ⅱ)当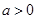 时,设
时,设 的最小值为
的最小值为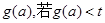 恒成立,求实数t的取值范围.
恒成立,求实数t的取值范围.
设函数
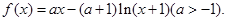
(Ⅰ)求
 的单调区间;
的单调区间;(Ⅱ)当
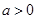 时,设
时,设 的最小值为
的最小值为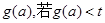 恒成立,求实数t的取值范围.
恒成立,求实数t的取值范围.(Ⅰ)当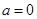 时,
时,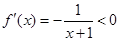 ,
,
所以函数 的减区间为
的减区间为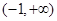 ,无增区间;
,无增区间;
当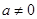 时,
时,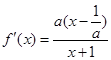 ,
,
若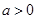 ,由
,由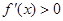 得
得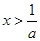 ,由
,由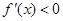 得
得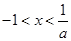 ,
,
所以函数 的减区间为
的减区间为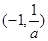 ,增区间为
,增区间为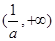 ;
;
若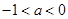 ,此时
,此时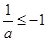 ,所以
,所以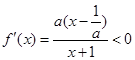 ,
,
所以函数 的减区间为
的减区间为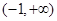 ,无增区间;
,无增区间;
综上,当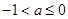 时,函数
时,函数 的减区间为
的减区间为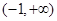 ,无增区间,
,无增区间,
当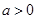 时,函数
时,函数 的减区间为
的减区间为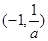 ,增区间为
,增区间为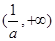 .
.
(Ⅱ)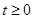 为所求.
为所求.
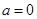 时,
时,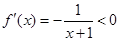 ,
,所以函数
 的减区间为
的减区间为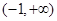 ,无增区间;
,无增区间;当
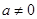 时,
时,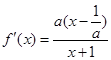 ,
,若
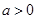 ,由
,由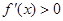 得
得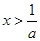 ,由
,由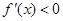 得
得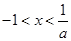 ,
,所以函数
 的减区间为
的减区间为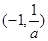 ,增区间为
,增区间为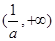 ;
;若
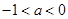 ,此时
,此时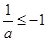 ,所以
,所以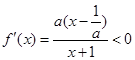 ,
, 所以函数
 的减区间为
的减区间为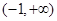 ,无增区间;
,无增区间;综上,当
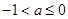 时,函数
时,函数 的减区间为
的减区间为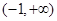 ,无增区间,
,无增区间,当
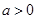 时,函数
时,函数 的减区间为
的减区间为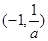 ,增区间为
,增区间为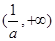 .
. (Ⅱ)
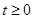 为所求.
为所求. (I)由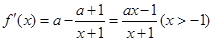 ,然后讨论a=0,a>0.-1<a<0.a<-1.a=-1等几种情况.
,然后讨论a=0,a>0.-1<a<0.a<-1.a=-1等几种情况.
(II)由(Ⅰ)得,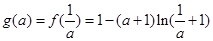 , 然后解本题的关键是根据
, 然后解本题的关键是根据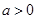 ,可得
,可得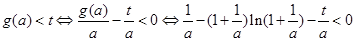 ,然后
,然后
令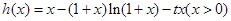 ,转化为不等式
,转化为不等式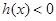 恒成立问题解决.根据导数进一步确定h(x)的最大值即可.
恒成立问题解决.根据导数进一步确定h(x)的最大值即可.
(Ⅰ)解: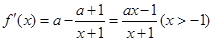 , ┄┄┄┄┄┄2分
, ┄┄┄┄┄┄2分
当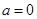 时,
时,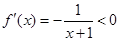 ,
,
所以函数 的减区间为
的减区间为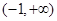 ,无增区间;
,无增区间;
当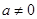 时,
时,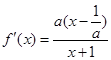 ,
,
若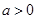 ,由
,由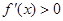 得
得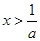 ,由
,由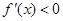 得
得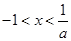 ,
,
所以函数 的减区间为
的减区间为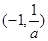 ,增区间为
,增区间为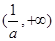 ;
;
若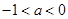 ,此时
,此时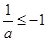 ,所以
,所以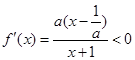 ,
,
所以函数 的减区间为
的减区间为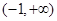 ,无增区间;
,无增区间;
综上,当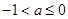 时,函数
时,函数 的减区间为
的减区间为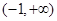 ,无增区间,
,无增区间,
当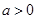 时,函数
时,函数 的减区间为
的减区间为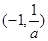 ,增区间为
,增区间为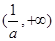 . …………6分
. …………6分
(Ⅱ)解:由(Ⅰ)得,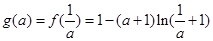 ,
,
因为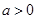 ,所以
,所以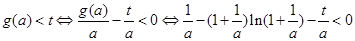 ,………8分
,………8分
令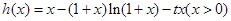 ,则
,则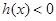 恒成立,
恒成立,
由于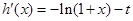 ,
,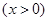
当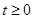 时,
时,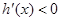 ,故函数
,故函数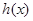 在
在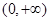 上是减函数,
上是减函数,
所以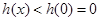 成立; ………10分
成立; ………10分
当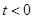 时,若
时,若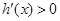 得
得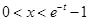 ,
,
故函数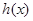 在
在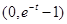 上是增函数,
上是增函数,
即对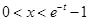 ,
,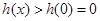 ,与题意不符;
,与题意不符;
综上,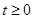 为所求. ………12分
为所求. ………12分
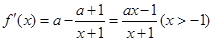 ,然后讨论a=0,a>0.-1<a<0.a<-1.a=-1等几种情况.
,然后讨论a=0,a>0.-1<a<0.a<-1.a=-1等几种情况.(II)由(Ⅰ)得,
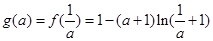 , 然后解本题的关键是根据
, 然后解本题的关键是根据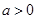 ,可得
,可得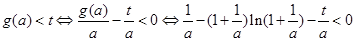 ,然后
,然后令
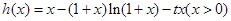 ,转化为不等式
,转化为不等式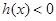 恒成立问题解决.根据导数进一步确定h(x)的最大值即可.
恒成立问题解决.根据导数进一步确定h(x)的最大值即可.(Ⅰ)解:
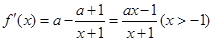 , ┄┄┄┄┄┄2分
, ┄┄┄┄┄┄2分当
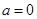 时,
时,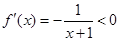 ,
,所以函数
 的减区间为
的减区间为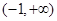 ,无增区间;
,无增区间;当
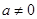 时,
时,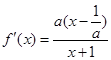 ,
,若
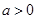 ,由
,由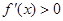 得
得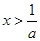 ,由
,由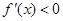 得
得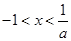 ,
,所以函数
 的减区间为
的减区间为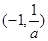 ,增区间为
,增区间为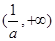 ;
;若
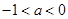 ,此时
,此时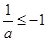 ,所以
,所以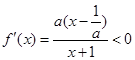 ,
, 所以函数
 的减区间为
的减区间为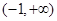 ,无增区间;
,无增区间;综上,当
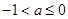 时,函数
时,函数 的减区间为
的减区间为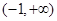 ,无增区间,
,无增区间,当
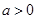 时,函数
时,函数 的减区间为
的减区间为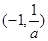 ,增区间为
,增区间为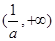 . …………6分
. …………6分(Ⅱ)解:由(Ⅰ)得,
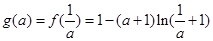 ,
, 因为
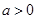 ,所以
,所以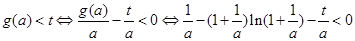 ,………8分
,………8分令
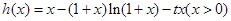 ,则
,则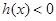 恒成立,
恒成立,由于
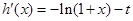 ,
,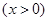
当
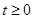 时,
时,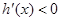 ,故函数
,故函数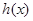 在
在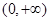 上是减函数,
上是减函数,所以
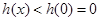 成立; ………10分
成立; ………10分当
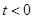 时,若
时,若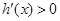 得
得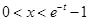 ,
,故函数
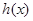 在
在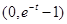 上是增函数,
上是增函数,即对
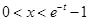 ,
,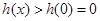 ,与题意不符;
,与题意不符;综上,
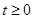 为所求. ………12分
为所求. ………12分
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
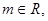 函数
函数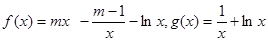
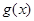 的最小值;
的最小值; 在
在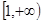 上为单调增函数,求实数
上为单调增函数,求实数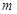 的取值范围;
的取值范围;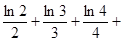 …
…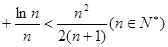 .
.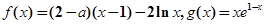 ,(
,(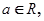 e为自然对数的底数)
e为自然对数的底数)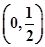 上无零点,求a的最小值;
上无零点,求a的最小值;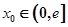 ,在
,在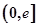 上总存在两个不同的
上总存在两个不同的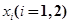 ,使得
,使得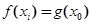 成立,求a的取值范围.
成立,求a的取值范围.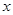 ,有
,有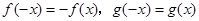 ,且
,且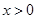 时,
时,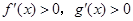 ,则
,则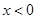 时( )
时( )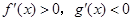
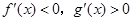
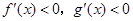
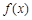 是定义在
是定义在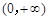 上的非负的可导函数,且满足
上的非负的可导函数,且满足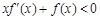 ,若
,若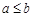 且
且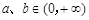 ,则
,则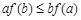
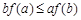


 ,定义
,定义 是
是 的导函数
的导函数 的导函数,若方程
的导函数,若方程 有实数解
有实数解 ,则称点
,则称点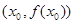 为函数
为函数 对称:
对称: 有实数解
有实数解 ,则,
,则,
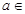 R,函数
R,函数 (x∈R).
(x∈R). 时,求函数f(x)的单调递增区间;
时,求函数f(x)的单调递增区间; 的取值范围;若不能,请说明理由;
的取值范围;若不能,请说明理由; 上单调递增,求
上单调递增,求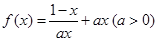 .
.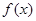 在
在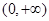 的单调性并证明;
的单调性并证明; 上的最小值。
上的最小值。