Question

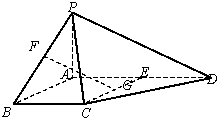
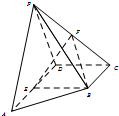
在四棱锥P-ABCD中，底面ABCD为直角梯形，BC∥AD，∠ADC=90°，BC=CD=

1

2

AD，PA=PD，E，F为AD，PC的中点．
（Ⅰ）求证：PA∥平面BEF；
（Ⅱ）求证：AD⊥PB．

Answer 1

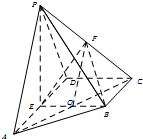
（Ⅰ）证明：连接AC交BE于O，并连接EC，FO，∵BC∥AD，BC=

1

2

AD，E为AD中点，∴AE∥BC，且AE=BC，∴四边形ABCE为平行四边形，…（1分）
∴O为AC中点．…（2分）
又∵F为AD中点，∴OF∥PA．…（4分）
∵OF?平面BEF，PA?平面BEF，…（5分）∴PA∥平面BEF． …（7分）
（Ⅱ）连接PE，∵PA=PD，E为AD中点，∴AD⊥PE．…（8分）
∵

BC∥AD，BC= 1 2 AD

，E为AD的中点，∴BCDE为平行四边形，∴BE∥CD．
∵AD⊥CD，∴AD⊥BE．

…

（9分）
∵PE∩BE=E，∴AD⊥平面PBE，…12分
∵PB?平面PBE，∴AD⊥PB． …14分