题目内容
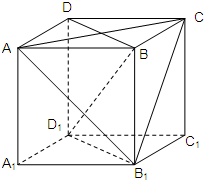
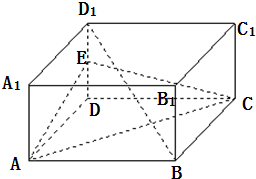
如图,在长方体ABCD-A1B1C1D1中,E是DD1的中点.
(1)求证:BD1∥平面ACE
(2)过直线BD1是否存在与平面ACE平行的平面,若存在,请作出这个平面与长方体ABCD-A1B1C1D1的交线(请在答题卡上用黑色碳素笔和直尺作图),并证明这两个平面平行;若不存在,请说明理由.
(1)求证:BD1∥平面ACE
(2)过直线BD1是否存在与平面ACE平行的平面,若存在,请作出这个平面与长方体ABCD-A1B1C1D1的交线(请在答题卡上用黑色碳素笔和直尺作图),并证明这两个平面平行;若不存在,请说明理由.

(1)证明:设AC∩BD=O,连接OE,
因为E是DD1的中点,O是BD的中点,
所以OE∥BD1.
又因为OE?平面ACE,BD1?平面ACE,
所以BD1∥平面ACE.
(2)存在.
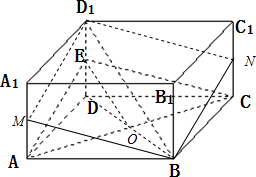
取AA1,CC1中点M,N,连接MD1,MB,BN,ND1,
因为E是DD1的中点,M是AA1的中点,所以AE∥D1E,
同理D1N∥CE.
因为D1E,D1N?平面D1MBN,AE,CE?平面ACE,
所以平面ACE∥平面D1MBN.
因为E是DD1的中点,O是BD的中点,
所以OE∥BD1.
又因为OE?平面ACE,BD1?平面ACE,
所以BD1∥平面ACE.
(2)存在.
取AA1,CC1中点M,N,连接MD1,MB,BN,ND1,
因为E是DD1的中点,M是AA1的中点,所以AE∥D1E,
同理D1N∥CE.
因为D1E,D1N?平面D1MBN,AE,CE?平面ACE,
所以平面ACE∥平面D1MBN.


练习册系列答案
 名师指导一卷通系列答案
名师指导一卷通系列答案
相关题目