题目内容
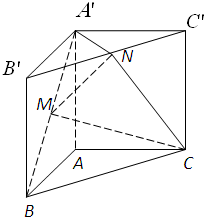
(文科)如图,正方体ABCD-A1B1C1D1中,M,N,E,F分别是棱A1B1,A1D1,B1C1,C1D1的中点,
求证:平面AMN∥平面EFDB.
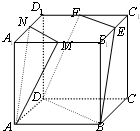
求证:平面AMN∥平面EFDB.

证明:如图所示,连接B1D1,NE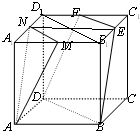
∵M,N,E,F分别是棱A1B1,A1D1,B1C1,C1D1的中点
∴MN∥B1D1,EF∥B1D1
∴MN∥EF
又∵MN?面BDEF,EF?面BDEF
∴MN∥面BDEF
∵在正方形A1B1C1D1中,M,E,分别是棱A1B1,B1C1的中点
∴NE∥A1B1且NE=A1B1
又∵A1B1∥AB且A1B1=AB
∴NE∥AB且NE=AB
∴四边形ABEN是平行四边形
∴AN∥BE
又∵AN?面BDEF,BE?面BDEF
∴AN∥面BDEF
∵AN?面AMN,MN?面AMN,且AN∩MN=N
∴平面AMN∥平面EFDB

∵M,N,E,F分别是棱A1B1,A1D1,B1C1,C1D1的中点
∴MN∥B1D1,EF∥B1D1
∴MN∥EF
又∵MN?面BDEF,EF?面BDEF
∴MN∥面BDEF
∵在正方形A1B1C1D1中,M,E,分别是棱A1B1,B1C1的中点
∴NE∥A1B1且NE=A1B1
又∵A1B1∥AB且A1B1=AB
∴NE∥AB且NE=AB
∴四边形ABEN是平行四边形
∴AN∥BE
又∵AN?面BDEF,BE?面BDEF
∴AN∥面BDEF
∵AN?面AMN,MN?面AMN,且AN∩MN=N
∴平面AMN∥平面EFDB

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目