题目内容
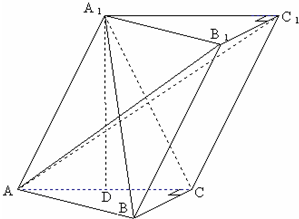
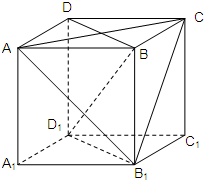
棱长为1的正方体ABCD-A1B1C1D1中,点M,N分别在线段AB1,BC1上,且AM=BN,给出以下结论:其中正确的结论的个数为( )
①AA1⊥MN
②异面直线AB1,BC1所成的角为60°
③四面体B1-D1CA的体积为
④A1C⊥AB1,A1C⊥BC1.
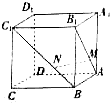
①AA1⊥MN
②异面直线AB1,BC1所成的角为60°
③四面体B1-D1CA的体积为
| 1 |
| 3 |
④A1C⊥AB1,A1C⊥BC1.
| A.1 | B.2 | C.3 | D.4 |

对于①,分别作NE⊥BC,MF⊥AB,垂足分别为E、F,连结EF
由AM=BN利用正方体的性质,可得四边形MNEF为平行四边形
∴MN∥EF,可得MN∥平面ABCD
∵AA1⊥平面ABCD,∴AA1⊥MN,因此可得①正确;
对于②,连结B1D1、AD1,可得∠B1AD1就是异面直线AB1,BC1所成的角
∵△B1AD1是等边三角形,∴∠B1AD1=60°
因此异面直线AB1,BC1所成的角为60°,得到②正确;
对于③,四面体B1-D1CA的体积为
V=VABCD-A1B1C1D1-4VB1-ABC=1-4×
=
,得到③正确;
对于④,根据A1B1⊥平面BB1C1C,得到A1B1⊥BC1,
由正方形BB1C1C中证出B1C⊥BC1,所以BC1⊥平面A1B1C,
结合A1C?平面A1B1C,得A1C⊥BC1,同理可证出A1C⊥AB1,从而得到④正确
综上所述,四个命题都是真命题
故选:D
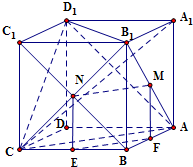
由AM=BN利用正方体的性质,可得四边形MNEF为平行四边形
∴MN∥EF,可得MN∥平面ABCD
∵AA1⊥平面ABCD,∴AA1⊥MN,因此可得①正确;
对于②,连结B1D1、AD1,可得∠B1AD1就是异面直线AB1,BC1所成的角
∵△B1AD1是等边三角形,∴∠B1AD1=60°
因此异面直线AB1,BC1所成的角为60°,得到②正确;
对于③,四面体B1-D1CA的体积为
V=VABCD-A1B1C1D1-4VB1-ABC=1-4×
| 1 |
| 6 |
| 1 |
| 3 |
对于④,根据A1B1⊥平面BB1C1C,得到A1B1⊥BC1,
由正方形BB1C1C中证出B1C⊥BC1,所以BC1⊥平面A1B1C,
结合A1C?平面A1B1C,得A1C⊥BC1,同理可证出A1C⊥AB1,从而得到④正确
综上所述,四个命题都是真命题
故选:D


练习册系列答案
 快捷英语周周练系列答案
快捷英语周周练系列答案
相关题目